高校入試確率の傾向と対策！定番問題はマスターしよう！

高校入試数学で、必ずと言っていいほど問われる「確率」。

しかし、「確率って分からない…」「全部書き出さないと解けないんじゃないの？」と思っている人、そして「そもそも確率って何？」と不安を抱えている人は多くいるのではないでしょうか。

そこで今回は、高校入試数学で出題される確率の傾向と対策について説明します。

直前に押さえるべき勉強法もまとめてあり、直前期で確率に関して焦っている！と言う人にも役に立つ記事になっているので、ぜひ参考にしてください。

そもそも確率とは？

はじめに、そもそも確率とは何かについて説明します。

確率とは、「ある事象が起こる割合」「どれくらい出やすいかを表す分数」のことをいいます。

確率の求め方は、「それが起こる場合/全体」です。

実際の問題を基に考えてみましょう。

(問)あたりが1本、はずれが４本の計5本のくじが袋に入っている。あたりを引く確率は？
(答)⅕

この問題での「全体」は全てのくじの本数の「5」であり、「それが起こる場合」は、この場合はあたりを引く場合なので「1」になります。

今回提示した問題は「簡単！」と思った人もいるかもしれませんが、「確率」は場合の数を理解していないと解けないものです。

では、場合の数とは何でしょうか。

場合の数とは？

場合の数とは、「ある事柄の起こりうる場合の総数」のことです。

例えば、サイコロを振って出る目の出方の総数「6」などが当てはまります。

つまり「何通りあるか？」というその数が、場合の数です。

どのような問題が出題されるのか

では、どのような問題が出題されるのでしょうか。

都立高校入試において、過去に出題された問題をみていきましょう。

平成29年度大問1(8)

(解答1)
大小2つのサイコロの出方は6×6=36(通り)
出る目の数の和が11以上になるのは、(大,小)=(5,6)(6,5)(6,6)の3通りのみです。
出る目の数の和が11以上になる確率は3/36=1/12。
故に、出る目の数の和が10以下になる確率は1-1/12=11/12。

この問題は、「2つの和が10以下になるものの数」が多いので、「和が11以上のものの確率」を求めて1から引いています。

このように、より求めやすい方を求めてから問われていることに答えるという方法もあるということは覚えておいてください。

(解答2)
サイコロ2つの問題は、以下のような表を書くと分かりやすくなります。
横が大きいサイコロの出る目、縦が小さいサイコロの出る目です。大小2個のサイコロの出方は36通りで、その目を足した数をマス内に書いています。

その中で、和が10以下のものは黄色い枠のものです。故に、全36通りのうち33通りが和が10以下なので、出る目の数の和が10以下になる確率は33/36＝11/12。

高校入試で色は使えないので、当てはまるものにチェックを入れたり、丸で囲んで分かるようにしましょう。

平成27年都立高校入試数学大問1(8)

【解答】
赤玉をR1,R2,R3、白玉をW1,W2と表すと、2個の玉の取り出し方は
(R1-R2)(R1-R3)(R1-W1)(R1-W2)(R2-R3)(R2-W1)(R1-W2)(R3-W1)(R3-W2)(W1-W2)の10通り。
そのうち、少なくとも1個は白玉の場合の数は7通り。
よって求める確率は7/10。

解答では全てを括弧書きで羅列しましたが、「見にくい…！」「分かりにくい…！」という人は樹形図を書いて解くことをお勧めします。

数えこぼしがないことが樹形図の利点なので、確率を不安に感じている人こそ、樹形図を用いて解きましょう。

高校入試に出やすい問題

高校入試に出題されやすい確率の問題は、以下の5つになります。

• サイコロを投げる問題/コインを投げる問題
• 箱の中から玉を同時に取り出す問題
• カードを用いて数字をつくる問題
• 色の塗り分け問題
• じゃんけん問題

これらの問題はみなさんも、教科書や参考書などで1度は見たことがあるかもしれません。

しかし、念のためもう一度解法を確認しておきましょう。

どのように勉強すればいいのか

次に、確率をどのように勉強すればいいのかについて解説します。

確率を勉強するStepは以下の3つです。

Step1.樹形図や表の書き方を理解する
Step2.定番の問題を解く
Step3.応用問題に取り組む

ではステップごとに1つずつみていきましょう。

Step1.樹形図や表の書き方を理解する

樹形図や表の書き方を理解しましょう。

樹形図とは、以下の図のようなものをいいます。

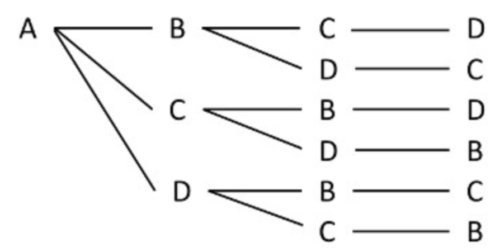
表は、先述の平成29年度大問1(8)のサイコロ問題で提示したようなものです。

それぞれ、教科書や参考書などに書き方が載っていると思うので、1度確認してみてください。

そして、書き方を理解したら、実際の問題でたくさん用いて書き慣れていきましょう。

Step2.定番の問題を解く

樹形図や表の書き方をマスターしたら、先ほど紹介した高校入試に出やすい確率の問題を解いてください。

• サイコロを投げる問題/コインを投げる問題
• 箱の中から玉を同時に取り出す問題
• カードを用いて数字をつくる問題
• 色の塗り分け問題
• じゃんけん問題

これらは、定番の問題になります。この問題の解法を完全に理解してから、次の応用問題を取り組みましょう。

Step3.応用問題に取り組む

Step2まで出来たら次は、応用問題です。

応用問題は、主にStep1とStep2を組み合わせることで解くことができます。

応用問題のみがまとめられている参考書もあるので、参考にしてみてください。

『最高水準問題集 数学2年』

直前だけど大丈夫！直前期の確率対策

「入試まで時間がないのに、確率が全然分からない…！」と焦っている人もいるでしょう。

そこで今回は、「直前期でも間に合う！確率対策！」について説明します。

直前期にすべきことは以下の2つです。

1. 過去問を解き、出題されやすい問題を把握する
2. 問題を解く際には、問題を正確に読み解く

では、それぞれ詳しくみていきます。

過去問を解き、出題されやすい問題を把握する

直前期には何よりも過去問を解くようにしてください。

「過去問は過去に出題されたものだから、同じものは出ないよ～」と思う人もいるでしょう。確かに同じ問題が出題されることは少ないです。

しかし、過去問を解くことで各自治体の問題傾向を知ることが出来ます。確率の分野だけの「過去問分析」をして、どのような問題が出やすいのか把握しましょう。

そして、過去問で出てきた問題と似たような問題を、みなさんが前々から使っていた参考書で探して解いてみてください。

解法定着のためには、何度も似たような問題に触れることが大切です。

問題を正確に読み解く

問題を正確に読み解くようにしましょう。

「条件は何か」「求めなくてはならないことは何か」などをきちんと理解してから問題に取り組んでください。

例えば、くじ引き問題であたりを引く確率が問われているのに、はずれを引く確率を求めてしまうなどは、間違いとしてよくあることです。

解法が分かっているのに関わらず、間違えてしまうことはとてももったいないですよね。

確率で計算ミスをしない方法

確率は、整理をするために数字をたくさん書き、問題によっては約分をする段階もあります。そのため、確率は計算ミスをしやすい分野です。

そこで今回は、確率で計算ミスをしない方法についてみていきます。

丁寧に樹形図や表を書く

丁寧に樹形図や表を書くようにしましょう。

その前にまずは、樹形図や図の書き方をきちんと身に付けてください。「こんなもんだろう！」と思って独自の書き方を生み出す前に、教科書や参考書などで「樹形図の書き方」を確認しましょう。

また、樹形図を書く際には、どのくらい書く必要があるかを予測して十分なスペースに書いてください。

表を書く際には、縦横の線をまっすぐ書きましょう。また印などを付ける場合は、印同士がこんがらがらないように注意が必要です。

数字を丁寧に書く

確率だけではなく数学を解く際全てに共通することですが、数字は丁寧に書きましょう。

例えば、「0と6」「1と7」などを急いで書くと、見分けがつかないことが多いです。

今一度自身の文字を見直してみてください。

また、字はある程度見やすい大きさで書くことが大切です。そのため、計算用紙のスペースの使い方には気を付けましょう。

約分をする際は、一気にしない

約分をする際には、一気にしないようにしましょう。

例えば「45/60=3/4」などのように、途中の15/20や9/12などをとばして計算することを「一気に約分する」といいます。

確かに一気に約分をすると多少解く時間は早くなります。しかし途中の計算を紙に残さないためミスをする可能性も上がるでしょう。そのため出来れば避けてほしいのですが、もし一気にする場合は十分に気を付けてください。

「計算ミスをなくしたい！」と考えている人は、以下の記事を参考にしてみてください。

まとめ

今回は、高校入試確率の傾向と対策についての解説をしました。

高校入試の確率は、各自治体によって基本的な問題から発展的な問題まで様々出題されます。

確率対策には、3Stepで確実に理解しましょう。そのステップを最後にもう一度確認します。

Step1.樹形図や表の書き方を理解する
Step2.定番の問題を解く
Step3.応用問題に取り組む

確率は出題されやすい問題がありますので、多くの問題を解いて理解してください。最後まで諦めずに対策をしましょう。