物体の運動のなかで最もシンプルなものが等速直線運動です。
いろんな運動を学んでいく上で基礎になる部分なので、しっかり押さえておきましょう。
等速直線運動とは
等速、つまり同じ速さで同じ向きに直線的に運動している様子を「等速直線運動」といいます。
等速直線運動をしている例として、カーリングのストーンなどが挙げられます。
動いている物体をスマホなどのカメラで一定の時間間隔で撮影したとき、写っている物体の間隔が一定であれば、それは等速直線運動です。

等速直線運動を解く上で覚えておきたいポイント!
等速直線運動の特徴と、物体が等速直線運動しているときの力のはたらきについて整理しましょう。
ポイント①速さについて理解する!
「一定の時間に物体が移動した距離」を、「速さ」といいます。
速さ、距離、時間は次の関係式で表されます。
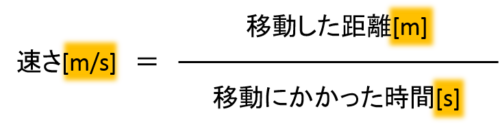
速さの単位は[m/s]と表し、「メートル毎(まい)秒」と読みます。
毎という漢字は、「まい」だけではなく「ごと」という読み方もあります。
「1秒ごと」とかの「ごと」という意味で、メートル毎秒は「1秒ごとに何メートル進むか」を表しています。
速さの単位はいろいろある
理科では速さを[m/s]という単位で表しますが、日常生活では他にも[cm/s]や[km/h]といった単位が使われています。
例えば、車で100km先の目的地に行きたいときに何時間かかるか考えたいときなど、mとsではわかりづらいときには[km/h]を使います。
いずれにせよ、速さの単位は[距離/時間]です。
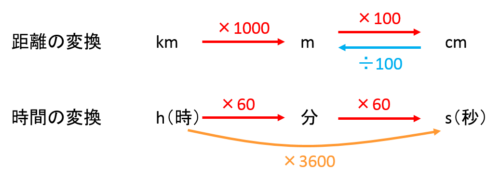
距離の単位[cm]や[km]から[m]へ、時間の単位[h]から[s]への変換はよく練習しておきましょう。
距離と時間をいっぺんに変換すると計算が複雑になってしまうので、それぞれで変換してから計算するとわかりやすくなります。
速さは向きを含まない
突然向きの話が出てきて驚いたかもしれませんが、物体が運動しているとき、物体は「ある方向に」運動していますよね?
例えば東京から北海道に向けてドライブしているとき、大ざっぱに言えば車は北に向かって運動しています。
ただし「時速60kmで動いている車」と言われても、北を向いて走っているのか東を向いているのかこれだけではわかりません。
つまり「速さという情報には運動の向きは含まれていない」のです。
では同じ時速60kmで動いている車が、北向きに走っていたけれど左折して東向きに走り出したとしましょう。
これは等速直線運動と言えるでしょうか?
左折しているので、直線上での運動ではありません。
よって、より正確には「等速直線運動=速さとその向きが変わらない運動」と言えます。
平均の速さと瞬間の速さ
ここでは、少し難しいですが「平均の速さと瞬間の速さ」について学びましょう。
今まで見てきた「時速60kmで動いている車」の速さは、「運動している間の車の平均の速さが60km/hである」ことを表しています。
実際には、信号待ちで停止するときや青信号になって発信するときなど、速さは変化しています。
こうしたそのときどきの速さを「瞬間の速さ」といいます。
速さが変化しているときは「等速」ではないので、急ブレーキや急発進のときは「等速直線運動をしていない」といえます。
ポイント②距離と時間の関係を整理しよう
等速直線運動では、運動している間の速さが一定です。
つまり、一定の距離を移動するのにかかる時間が一定なので、距離と時間は比例します。
これをグラフにすると次のようになります。
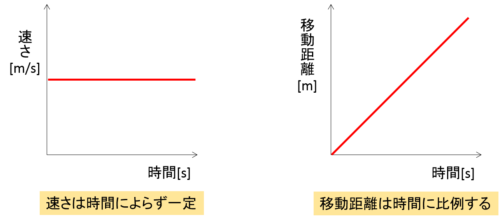
グラフの形と一緒に、等速直線運動では
- 時間が変化しても速さは変わらない
- 運動した時間に比例して移動距離が増える
ことを覚えておきましょう。
ポイント③力のはたらきと運動の関係を押さえる
さて、物体が運動するのは物体に力がはたらくからでしたね。
では物体が等速直線運動しているとき、物体にはどんな力がはたらいているのでしょうか?
答えは、
- 力がはたらいていない
- 2つ以上の力がはたらいているが、つり合っている
のどちらかです。
例えば、カーリングのストーンを手放すとストーンには外からの力がはたらかないように、等速直線運動では運動の向きに力がはたらいていません。
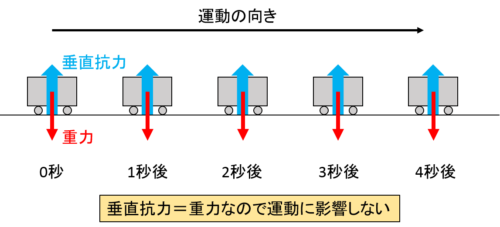
そして下の図のように、物体には必ず重力がはたらいていますが、重力は垂直抗力とつり合っています。
このように2つ以上の力がはたらいていてもつりあっているときは運動に影響しないので、物体の速さは変化しません。
この後の単元で習う自由落下では、運動の向きに一定の力がはたらき続けます。
自由落下とは持っていたボールから手を自然に離したときに起こるような運動で、手を離したあとのボールには重力がずっとはたらき続けます。
その場合物体の速度は一定の割合で大きくなるので、等速直線運動にはなりません。
実際は摩擦力や空気の抵抗のように運動とは反対の力がはたらくことが多いですが、その場合も「はたらく力がつり合っていれば等速直線運動」、そうでなければ違う運動になります。
あくまでも、等速直線運動では
- 力がはたらいていない
- 2つ以上の力がはたらいているが、つり合っている
のいずれかに該当するということを押さえておきましょう。
実際にどのような問題が出題されるのか?
さて、それでは実際の入試問題を解いてみましょう。
以下の問題は、平成30年度都立高校入試の大問1から抜粋したものです。
”水平な台の上で一直線上を運動している力学台車の運動を、1秒間に50回打点する記録タイマーを用いて記録したところ、図6のようになった。
図6の記録テープに位置Aと位置Bを付け、位置Aから位置Bまでの間隔を測定したところ5cmであった。
記録した位置Aから位置Bまでの力学台車の運動と、平均の速さを組み合わせたものとして適切なのは、次の表のア~エのうちではどれか。”
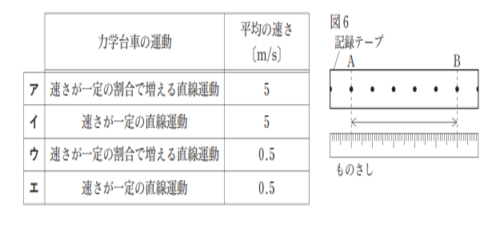
では、早速解いていきましょう。
記録テープの打点が等間隔で並んでいるので、この力学台車が一定の時間に進む距離、すなわち速さは変化していません。
よって、力学台車の運動は「速さが一定の直線運動」(等速直線運動)です。
続いて位置Aから位置Bまでを見ると、位置Aから始まって5打点で位置Bに到達しています。
ここでは1秒間に50回打点する記録タイマーを用いているので、5回打点するのにかかった時間は0.1秒(s)です。
位置Aから位置Bまでの間隔は5cm=0.05mなので、この間の平均の速さは
0.05m÷0.1s=0.5m/s
よって、答えはエとなります。
等速直線運動の勉強方法について
問題の感覚がつかめたところで、勉強方法をまとめましょう。
物体にはたらく力を描き出そう!
先ほどの過去問は等速直線運動単体での出題でしたが、実は等速直線運動の問題は斜面上の運動など他の運動と組み合わされて出題されることも多いです。
記録タイマーやストロボ写真のように「物体が等速直線運動をしているな」と目で見て判断できるときは良いのですが、そうでないときが厄介です。
物体が等速直線運動をしているかどうか見極めるには、物体にはたらく力を図に描けるかどうかが重要です。
これは他の運動を理解するにも大切なテクニックなので、しっかり練習しておきましょう。
等速直線運動の直前対策法!
それでは具体的に、等速直線運動の直前対策としてどのようなことに取り組めば良いのでしょうか?
他の運動と組み合わせて解けるようにする!
先述のとおり、等速直線運動の問題は他の運動と組み合わされて出題されることも多いです。
よく組み合わされるのは、斜面上の運動やエレベーターの運動といった、直線上で速さが変化する運動です。
運動の種類によって解き方が異なるので、そのとき物体がどんな運動をしているのかきちんと判断できることが大切です。
そのため、自分に合った問題集などで他の運動と組み合わされている設問に取り組み、様々なパターンに慣れておきましょう。
単位間違いに注意!
ポイント①で述べたように、速さの単位はいつも[m/s]とは限りません。
[cm/s]や[km/h]からの単位換算を改めて確認しておきましょう。選択肢には計算ミスで選びやすい誤答が並んでいることも多いので、単位の換算ミスには十分に注意しましょう。
最後に単位換算しようと考えていると、数字を見て安心して単位換算を忘れてしまうこともあり得ます。
速さを計算し始める前に、距離を[m]に、時間を[s]に揃えることを習慣化しましょう。
まとめ
等速直線運動は、物理分野で最初に出てくる運動の種類です。
他の運動と組み合わされた複雑な問題にも臆さず挑めるよう、ここでしっかり理解しておきましょう!














