多くの自治体の高校入試で必ずと言っていいほど出題される「規則性の問題」。
しかし、「全部書くしか方法はないの?」「規則性を見つけられない!」などと悩んでいる人も多くいるはずです。
そこで今回は、高校入試数学で出題される規則性の傾向と対策について説明します。
直前に押さえるべき勉強法もまとめており、直前期で規則性に関して焦っている!と言う人にも役に立つ記事になっているので、ぜひ参考にしてください。
そもそも規則性とは?
はじめに、そもそも規則性とは何かについて説明します。
規則性とは、「何らかの現象や状況に、一定のルールやパターンまたは規則などが認められるような性質、または状況のこと」です。
どのような問題が出題されるのか
では、どのような問題が出題されるのでしょうか。
都立高校入試において、過去に出題された問題をみていきましょう。
・都立高校平成29年度入試大問2(1)

【解答1】
10段まで全て書きだしましょう。
求めなくてはならない数は「右から2番目の数」なので、各段右から2番目の数字のみを書きだしましょう。
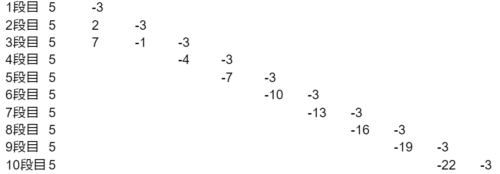
よって答えは-22のア。
【解答2】
4段目以降の右から2つ目のマスに入る数は、順に
4段目 -3+(-1)=-4
5段目 -3+(-4)=-7
・・・
と3ずつ減っていることが分かります。
よって右から2つ目のマスに入る数字は、6段目が-10、7段目が-13、8段目が-16、9段目が-19となり、10段目は-22となることが分かります。
・都立高校平成29年度入試大問2(2)

【解答】
証明
5段目の6個のマスに入っている数をそれぞれ a、b を用いた式で表すと、
左から、a、4a+b、6a+4b、4a+6b、a+4b、b となり、
その和は、a+(4a+b)+(6a+4b)+(4a+6b)+(a+4b)+b=16a+16b=16(a+b)
となる。
また、1 段目の2個のマスに入っている数の和は a+b と表せる。よって、5段目の6個のマスに入っている数の和は、1段目の2個のマスに入っている数の和の16倍となる。
(採点のポイント)
東京都教育委員会は、採点のポイントとして以下をあげている。
・5 段目の 6 個のマスに入っている数が、それぞれ a、b を用いた式で適切に表されているか。
→a、4a+b、6a+4b、4a+6b、a+4b、b
・式の変形ができ、適切に処理されているか。
→ a+(4a+b)+(6a+4b)+(4a+6b)+(a+4b)+b=16a+16b=16(a+b)
・5 段目の 6個のマスに入っている数の和が、1 段目の 2 個のマスに入っている数の和の16 倍になることが的確に示されているか。
→1 段目の2個のマスに入っている数の和は a+b と表せる。
よって、5段目の6個のマスに入っている数の和は、1段目の2個のマスに入っている数の和の16倍となる。
参考サイト:数学採点のポイント
よく出題される問題
規則性には、よく出題される問題があります。それは以下の3つです。
- マッチを並べる問題
- 正方形を並べて図形を作っていく問題
- 数字をある規則にそって並べていく問題
これらの問題はみなさんも、教科書や参考書などで1度は見たことがあるかもしれません。
しかし、念のためもう一度解法を確認しておきましょう。
どのように考えればいいのか
次に、規則性をどのように考えればいいのかについて解説します。
規則性を考えるStepは以下の3つです。
Step1 問題文を丁寧に読む
Step2 規則性を見つける
Step3 nを使って式で表す
では、各ステップごとに詳しくみていきましょう。
Step1.問題文を丁寧に読む
まず、問題文を丁寧に読みましょう。
多くの規則性の問題は問題文が長いため、読みたくなくなるという人も多くいるでしょう。
しかし、問題文を理解することが、問題を解く上で何よりも大切です。問題文を理解しなければ何を求めればいいのか分かりませんよね。
また、規則性の問題は問題文の中にヒントが書いてあります。
そのため「問題文が長くていやだ…」と思わずに、一旦読んでみてください。またその際に、書いてあることを図や表で視覚化しながら読むと、難しいという気持ちも薄れるはずです。
Step2.規則性をみつける
次に規則性をみつける作業です。
規則性をみつけるためには以下の4つの方法が考えられます。
- 図を分けて考える
- 表を書く
- 1つ1つ式を書きだす
- 変化する数とnとの関係をみつける
上記の4つのうちどの方法が適しているのかは、それぞれの問題によって異なります。
例えば、先述した都立高校平成29年度入試大問2(1)では「表を書く」ことが有効でしたよね。
また、都立高校平成29年度入試大問2(2)では、5段目の6個のマスに入っている数の式を「1つ1つ式を書きだす」ことで解答を導けます。
どの方法で解けばいいのかぱっと思いつかない場合は、順に試してみてください。
Step3.nを使って式で表す
最後にnを使って式で表しましょう。
このことは実際の数字を用いて、式を考えてみることで見いだせます。
具体的な数字を文字に変換することで規則性の式を導けたといえるので、最後まで頑張って解きましょう。
直前だけど大丈夫!直前期の規則性対策!
「入試まで時間がないのに、規則性が全然分からない…!」と焦っている人もいるはずです。
そこで今回は、「直前期だけど大丈夫!規則性対策!」について説明します。
直前期にすべきことは以下の2つです。
- 出題されやすい問題を解く
- 過去問で、規則性の問題をたくさん解く
出題されやすい問題を解く
出題されやすい問題を解きましょう。
出題されやすい問題は、先述した通り以下の3つです。
- マッチを並べる問題
- 正方形を並べて図形を作っていく問題
- 数字をある規則にそって並べていく問題
同じ問題は滅多に出ませんが、規則性の「見つけ方」「考え方」を学ぶことができます。
過去問で規則性の問題をたくさん解く
過去問で規則性の問題を多く解きましょう。
しかし、受験する都道府県の過去問だけではあまり問題数がないので、他の都道府県の入試問題もみてみることも有効です。
問題を解く際には「考え方」を学ぶことが大切なので、1回自分で考えてから解答を見るようにしましょう。
規則性の問題を解く上での注意点
最後に、規則性の問題を解く上での注意点をあげます。
注意点は主に2つです。
- 書きだして解けそうな問題ならば、書きだそう
- あまり時間をかけすぎない
書き出して解けそうな問題ならば、書き出そう
規則性を見つけることはもちろん大切です。
規則性を導かなければ解くことのできない問題も多々あります。
しかしその一方で、書き出して解ける問題もあります。検討する数が少なくて済む場合には、有効的です。もし、規則性を考えても思いつかなかった場合、書き出してみてください。
あまり時間をかけすぎない
もし規則性を見つけられなかった場合に何分も考えるのはもったいないです。なぜなら、規則性の証明問題などは、大体の都道府県で正答率が低いからです。
そのため、1回とばして時間が余ったらもう1度考えてみるという方法をおすすめします。
規則性の問題は、執着しすぎないことが大切です。正答率の低い問題に時間をかけるよりも、確実に解ける問題を解いていきましょう。時間配分を考えながら解くようにしてください。
しかし、数学を得点源にしたいと考えている人は、規則性の問題を解けるか否かで合否が決まることもあるでしょう。
自分の全教科のバランスを考えた上で判断してくださいね。
まとめ
今回は、高校入試規則性の傾向と対策についての解説をしました。
高校入試の規則性は、各自治体によって基本的な問題から発展的な問題まで様々出題されます。
規則性を考える際は、3Stepで取り組みましょう。そのステップを最後にもう一度確認します。
Step1 問題文を丁寧に読む
Step2 規則性を見つける
Step3 nを使って式で表す
規則性には出題されやすい問題がありますので、多くの演習を重ねて理解してください。最後まで諦めずに対策をしましょう。














