「角度を求めるのがニガテ…ましてや円周角なんて…」と思う中学生は多いと思います。
でも、円周角は一度掴んでしまえば得点源にしやすいシンプルな分野。悩みを抱えている中学生をお助けしたいと思い、今回は「受験で勝つための円周角必勝法」をお伝えします。
円周角・中心角とは?
円周角の問題を解くにあたり、言葉の定義から皆さんにお伝えします。
円周角とは
では、ます円周角の定義からお伝えします。一言で表すならば「円周角」とは「円周上の1点から、この点とは異なる円周上の2点を結んだ時にできる角度」のことです。
こちらが上記の言葉を表した図です。

弧ABに対する円周角Xであるため、この場合は円周角を∠AXBと表します。
中心角とは
続いて中心角の定義をお伝えします。一言で表すならば「中心角」とは「円の二つの半径が挟む角」のことです。
こちらが上記の言葉を表した図です。
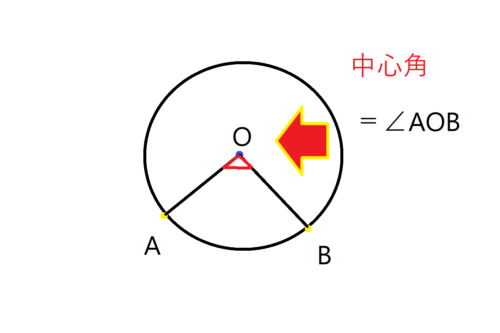
弧ABと半径AOと半径BOで成り立つ角度であるため、この場合は中心角を∠AOBと表します。
円周角の定理の重要ポイント
「円周角の定理」という言葉をよく耳にすると思いますが、いざ説明しようとしてもなかなか正確に説明することは難しいと思います。
そこで、今回は端的にポイントを絞ってお伝えします。
「円周角の定理」とは、「円周角のルール」です。ひらがなは「あ」の次が「い」でその次が「う」ですね。そのくらい簡単で絶対的で重要なルールです。
主に3つあります。
- 1つの弧に対する円周角の大きさは中心角の半分である
- 同じ弧に対する円周角は等しい
- 直径に対する円周角は90°
1つの弧に対する円周角の大きさは中心角の半分である
では1つ目の「1つの弧に対する円周角の大きさは中心角の半分である」から見ていきましょう。

弧ABから成り立つ円周角と中心角は、このような式が必ず成り立ちます。例えば、∠APBが60°だった場合、∠AOBは120°です。
これが、円周角の定理の「同じ弧に対する円周角と中心角のルール」です。
同じ弧に対する円周角は等しい
では2つ目の「同じ弧に対する円周角は等しい」を見てみましょう。

同じ弧ABから成り立つ円周角は、このような式が必ず成り立ちます。例えば、∠AXBが60°だった場合、∠AYBも60°です。
これが、円周角の定理の「同じ弧に対する円周角のルール」です。
直径に対する円周角は90°
最後に3つ目の「直径に対する円周角は90°」をお伝えします。
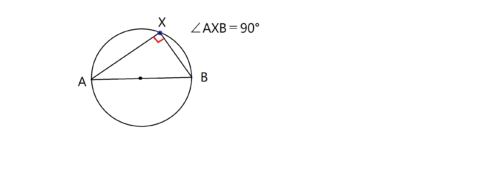
直径ABに対する円周角∠AXBは、必ず直角になります。
先ほどご紹介した「1つの弧に対する円周角の大きさは中心角の半分である」というルールから、直径ABに対する中心角が180°だから、円周角その半分の90°であるという事がわかりますね。これを知っているだけで格段に覚えやすいと思います。
これが、円周角の定理の「直径に対する円周角のルール」です。
都立高校の入試で円周角はこう出る!~円周角の出題パターン~
ここまで言葉の定義やルールを確認してきましたが、解けるようにならなければ意味はありません。
実際にどのような出題パターンがあるのでしょうか?都立高校の過去の入試問題を用いてご紹介しますので、皆さんも一緒に考えながら取り組んでみてください。
たとえば東京都立高校の共通試験では、2018年の問題4で円の総合問題が出題されました。
この年の問題のポイントは主に3つです。
- 円周角の定理
- 円と弧の長さ
- 円と三角形
ここでは「第1問」「第2問」を解説します。どちらの問題も、同じ図1を基にして問題が作成されています。
こちらが図1と、それに対する実際の問題文です。
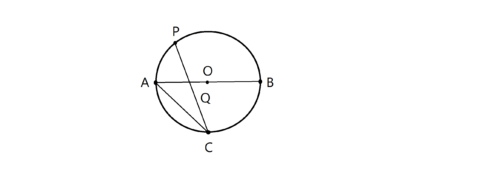
”図1で、点Oは線分ABを直径とする円の中心である。
点Cは円Oの周上にある点で、弧AC=弧BC である。
点Pは、点Cを含まない 弧AB 上にある点でA、点Bのいずれにも一致しない。
点Aと点C、点Cと点Pを、それぞれ結び、線分ABと線分CPとの交点をQとする。
次の各問に答えよ。”
早速第1問から見ていきましょう。
【第1問】
図1において ∠ACP= a°とするとき、
∠AQPの大きさを表す式を、次のア~エのうちから選び記号で答えよ。
ア(60−a)°
イ(90−a)°
ウ(a+30)°
エ(a+45)°
【第1問・解説】
大切なポイントは、先ほどご紹介した円周角の定理の3番目の「直径に対する円周角は90°」のルールを有効的に使うことです。

このことを踏まえ、補助線を引きます。そうすると直径ABに対する円周角∠ACBは直角になります。
さらに弧AC=弧BCという条件を踏まえると、∠CAB=∠ABA=45° となる。

円の性質により、∠AQP=∠CQBが成り立つ。
∠CQBの大きさを求めるために△CQBで考える。
∠CQB=180°-(∠QCB+∠QBC)
∠CQB=180°-{(90°-a°)+45°}
∠CQB=(a+45)°
よって答えは【エ】になります。
いかかでしょうか?解けましたか?
続いて第2問です。
【第2問】
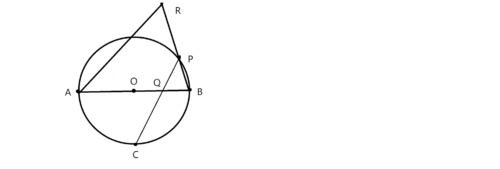
図2は、図1において、点Aと点P、点Bと点Pをそれぞれ結び、線分BPをPの方向に延ばした直線上にありBP=RPとなる点をRとし、点Aと点Rを結んだ場合を表している。
次の①、②に答えよ。
① △ABP ≡△ARP であることを証明せよ。
② 次の◻の中に当てはまる数字を答えよ。
図2において点Oと点Pを結んだ場合を考える。
弧BC=弧2BPのとき
△ACQの面積は、四角形AOPRの面積の◻倍である。
【第2問①・解説】
ここで大切なポイントは、先ほどご紹介した円周角の定理の3番目の「直径に対する円周角は90°」のルールです。
第一問と同様ですね。いかにこのルールが入試において重要かがわかります。
また、これは円の問題ですが『三角形の合同条件』を有効的に利用して解きます。

問題文より
①BP=RP
さらに共通の辺により
➁AP=AP
また∠APBは『直径ABに対する円周角』のため90°となる。
∠APR=180°‐90°=90°
よって
➂∠APB=∠APR
①~➂より
『三角形の二辺とその間の角が等しい』ので
△ABP ≡△ARPとなる。
証明終了
このように『円』と『三角形』の性質を問う融合問題でした。
【第2問➁・解説】

こちらは『面積比』の問題になります。ポイントは『円周角の定理の全ての条件』と『三角形の相似』を有効的に使うことです。
上の図のオレンジの四角形と緑の三角形の面積比を求めます。しかし、いきなり値を求めることはできません。
よって周辺の図形を利用して求めていきます。
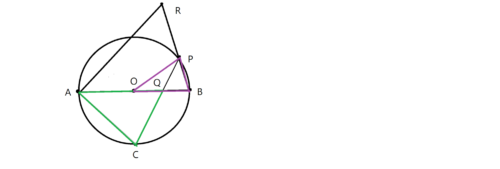
まずは△ACQと△OBPから見ていきます。
問題文より
弧BC=2弧BP
なので、
弧BC:弧BP=2:1
円周角CAB:円周角BAP=2:1
△ABCは直角二等辺三角形より、円周角CABは45°なので
円周角CAB:円周角BAP=45°:22.5°
中心角BOPは円周角BAPの2倍なので45° ①
△BOPは円Oの半径により辺OP=辺OB
これらにより、△BOPは二等辺三角形
このことから、∠OBPは67.5°
先ほどお伝えした円周角の定理の2番目の「同じ弧に対する円周角は等しい」というルールにより、円周角ACP=円周角ABP=67.5° ➁
①➁の条件により、「三角形の二つの角がそれぞれ等しい」ので
△ACQ∽△OBP
さらにこれから辺の比を求めます。

先きほど円周角PABは22.5°と求めました。
さらに円周角の定理の2番目の「同じ弧に対する円周角は等しい」というルールにより、
円周角PAB=円周角PCB=22.5°
線分OCを引くと
円周角の定理の3番目の「直径に対する円周角は90°」というルールにより、
△OBCは直角二等辺三角形なので∠OBC=45°

線分OCは半径なのでrと置きます。
直角二等辺三角形の比は1:1:√2であるから
辺OB:辺OC:辺BC=r:r:√2r=1:1:√2
∠OCQ=∠BCQ=22.5°なので
直線CQは角の二等分線です。
このことにより、線分OC:線分BC=線分OQ:線分BQ=1:√2

線分AO=線分BO=線分OQ+線分BQにより
辺AO:辺OQ:辺BQ=1+√2:1:√2
辺AQ:辺OB=1+√2+1:1+√2=2+√2:1+√2
先ほど△OBP∽△ACQを求めましたね。
このことにより、「辺の比」は2+√2:1+√2
よって「面積の比」は(1+√2)²:(2+√2)²
これを解くと△OBP∽△ACQ=1:2
ここまで周辺の図形を利用して辺の比や面積比を求めてきました。
そしてここからは本題の△OBP:□AOPRを求めましょう。
辺AO=辺BOにより
△OBP:△OAP=1:1
△OBP:△ABP=△OBP:△OBP:△OAP=1:1+1=1:2
△OBP:△ABR=△OBP:△ABP×2=1:2×2=1:4

このことにより△OBP:△ACQ:△ABR=1:2:4
従って△OBP:△ACQ:□AOPR=△OBP:△ACQ:△ABR‐△OBP=1:2:3
よって△ACQの面積は□AOPRの面積の2/3倍である。
答え:2/3倍
いかがでしたでしょうか?かなり難易度が高かったと思います。
しかし「円周角の定理」をうまく使うことができれば解けるようになっています。解けなかった方はもう一度円周角のルールを確認してみましょう。
円周角の問題が解けるようになるためには?
ここまで円周角を詳しく見てきましたが、どのようにしたら「円周角が得意!」と言えるようになるのでしょうか?
それを言えるようになるためには「円周角の定理をパッと言えるようになること」が必要です。これができる人は円周角の問題で高得点を取ることができます。
皆さんは「円周角の定理を全て説明してください」と言われたらパッと的確に説明できますか?
できない方はすぐに確認してください。できる方は、定理の証明まで言えるとさらに良いです。
どんなに難しい問題でも「円周角の定理」がベースでできています。だからこそ、このベースを完璧にしておけばどんな問題にも対応できます。
また「演習量」も重要です。どんな問題にも対応できるように、様々な傾向の問題に出会うことも非常に重要です。
そこで、演習量を積むためにおすすめの参考書はこちらです。
『最高水準特進問題集 数学3年 ([新学習指導要領対応])』
この参考書で「円周角と中心角」の問題があるのでチャレンジしてみてください。比較的難易度は高いです。入試の実践レベルまで解けるようになりたい方におすすめです。
まとめ
円周角についてたくさん見てきましたが、いかがだったでしょうか?「円周角の定理」を制す者は「円周角・中心角」を制します。今回の内容をしっかりと復習して円周角マスターになりましょう!














