高校入試の平方根をたった3分で「得意」にする方法！

中学3年生で勉強する「平方根」。

ルートの記号が新しくでてくる上にプラスとマイナスや記号で混乱してしまう中学生が多く、理解できるまでは混乱してしまう分野です。

そのため、受験生としてのスタートダッシュを気持ち良く行うことができないのです。

しかしコツさえ掴めば、誰でも「平方根の問題が得意だ」と堂々と言えるようになります。今回はそのコツを皆さんにお伝えします。

平方根とは

そもそも「平方根」とは何なのでしょう？

「平方根」は「二乗の逆」と覚えてください。とても覚えやすいですね。

★とAで「平方根」を確認しましょう。

「平方根」は「二乗の逆」なので、二乗してAになる数（★）はAの「平方根」ということになります。具体的に数値を用いて見てみましょう。

二乗したら25（A）になる数（★）は何でしょう？

5と－5ですね。つまり、25の平方根は5と－5になります。

そして25を「平方数」といいます。平方数とは自然数の二乗で表される整数のことを指します。

「2つもあるの？」とびっくりする方がいるかもしれません。しかし、これは「平方根の性質」なのです。平方根は基本的に2つあるという事を忘れないでください。

次は「平方根の性質」について詳しく見ていきます。

平方根の性質

先ほどお伝えした「平方根はいつも2つある」という性質についてもっと詳しく、さらに他の性質についても詳しくお伝えします。

主に5つあります。

• 記号は「√」を使う
• 「平方根」はプラスとマイナスの2つが存在して絶対値はそれぞれ等しい
• 0の平方根は0である
• 負の数の平方根は存在しない
• 「√」の中は必ず0以上

ひとつひとつ見てみましょう。

記号は「√」を使う

「平方根」は「√」という記号を用いて表します。

先ほどの「二乗したら25（A）になる数（★）は何でしょう？」という例だと25の平方根は5と－5になりますが、いつでも「平方根」を整数で表すことはできません。

例えば、2の平方根は何でしょう？という問題があったとします。

その場合、「二乗したら２になる数字って…？」と混乱すると思います。

二乗したら2になる整数はありません。そんな時に救世主となってくれるのが「√」という記号です。読み方は「ルート」、別名「根号」です。

よって正解は「±√2」になります。「プラスマイナス　ルート2」と読みます。

「平方根」はプラスとマイナスの2つが存在して絶対値はそれぞれ等しい

先ほどお伝えしました性質ですね。さらに詳しく確認しましょう。

（★）²=25　★=5、-5
（★）²=2 ★=√2、-√2

皆さんは、ここから気づくことはありますか？

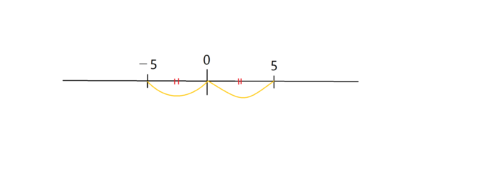
5と-5、√2と-√2はそれぞれ0からの距離が等しいです。つまり、平方根は絶対値が同じなのです。

とても重要な性質なので覚えてください。

0の平方根は0である

二乗して0になる数は0のみです。つまり、0の「平方根」は0のみです。

負の数の平方根は存在しない

例を用いて一緒に考えてみましょう。

（★）²=-25

中学数学においては、二乗して-25になる数値は決して存在しません。よってこの等式は成り立ちません。

必ず「平方根」の中は正の数になります。

「√」の中は必ず0以上

37の平方根=±√37
23の平方根=±√23
17の平方根=±√17

このように「√」の中は必ず「正の数」になります。負の数になることは決してありません。

先ほど0の平方根は0とお伝えしましたが、√0という書き方も成り立つので「√の中は0以上」というルールになっています。

高校入試の平方根の計算でおさえるポイント

ここまで読んで平方根の性質を十分に理解できたと思います。次は実際に平方根の計算をやっていきましょう。

その前におさえてほしいポイントがあります。それは「√の中身を簡単にする必要がある」「分母の有理化を行いルートを無くす」ということです。

ルートの中身を簡単にする

例えば√20は中身を簡単にする必要があります。それはなぜでしょうか？

それは√20の中に「平方数」が含まれているからです。

因数分解すると

になります。この赤線で引いた部分が4、つまり「平方数」です。

平方数は√の外に出して整数にしなければなりません。下記のようになります。

解答をする場合は必ず「最も簡単にした状態」で答えなければ不正解として扱われてしまうので気をつけましょう。

有理化

「有理化」とは「分母のルートをなくす」作業のことをいいます。

では5/√5を有理化してみましょう。

とにかく「分母から√を取り去る」ことを考えれば良いので、分母と分子に√5をかけます。

分母と分子両方に、分母と同じ値の√をかけたら、そのあとは単純な計算です。

こちらも解答をする場合は必ず「有理化された状態」で答えなければ不正解として扱われてしまうので気をつけましょう。

具体的な平方根の計算方法について

それでは実際に計算の方法をご紹介します。

平方根の足し算・引き算

平方根の足し算・引き算のポイントは3つあります。

1. ルートの中を最も簡単な数字にする
2. ルートの中が同じ数字のみ計算する
3. ルートの外の整数部分のみ計算する

この3つです。これさえおさえておけば大丈夫です。

それでは、具体的にどういう形になるのかを確かめるために、

“√18+√162－√108”

を解いてみましょう。

まず、ポイントの1つ目「ルートの中を最も簡単な数字にする」を行います。

√18+√162－√108
=3√2+9√2－6√3

続いて、ポイントの2つ目「ルートの中が同じ数字のみ計算する」と3つ目の「ルートの外の整数部分のみ計算する」を行います。

√2と√3は中身のルートの数が異なるので計算してはいけません。

例えば、√2+√3=√5　にはなりません。

√18+√162－√108
=3√2+9√2－6√3
=12√2－6√3

続いて掛け算も見ていきましょう。

平方根の掛け算

掛け算のポイントは3つあります。

1. ルートの中を最も簡単な数字にする
2. 整数同士・ルートの中同士をかける
3. かけあわせたルートの中を最も簡単な数字にする

この3つです。これさえおさえておけば大丈夫です。

“√20×√60”

を解いてみましょう。

まず、ポイントの1つ目「ルートの中を最も簡単な数字にする」を行います。

√20×√60
=2√5×2√15

続いてポイントの2つ目の「整数同士・ルートの中同士をかける」を行います。

√20×√60
=2√5×2√15
=4√75

続いてポイントの3つ目の「かけあわせたルートの中を最も簡単な数字にする」を行います。

√75は、5√3です。整数の4と掛け合わせます。

√20×√60
=2√5×2√15
=4√75
=20√3

続いて割り算も見ていきましょう。

平方根の割り算

割り算のポイントは3つあります。

1. ルートの中を最も簡単な数字にする
2. 分数にしてルートでくくる
3. 分母を有理化する

この3つです。これさえおさえておけば大丈夫です。

“√63÷√18”

を解いてみましょう。

まず、ポイントの1つ目「ルートの中を最も簡単な数字にする」を行います。

√63÷√18
=3√7÷3√2

続いてポイントの2つ目の「分数にしてルートでくくる」を行います。

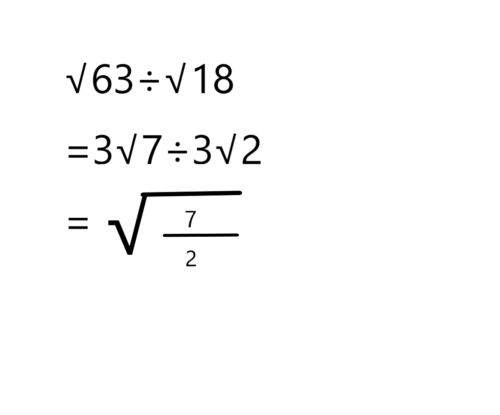
続いてポイントの3つ目の「分母を有理化する」を行います。

分母の有理化についてわからなくなった場合は、この記事を遡ってもう一度確認しましょう。

有理化して答えは

=√14/2　になります。

平方根の出題傾向

では、実際の入試問題で「平方根」の出題パターンを確認しましょう。

都立高校の過去の入試問題を用いてご紹介しますので、皆さんも一緒に考えながら取り組んでみてください。

たとえば東京都立高校の共通試験では、2020年の大問1の問3で平方根の計算問題が出題されました。

こちらです。

“（2－√6）（1+√6）を計算せよ。”

比較的簡単な問題ですので、皆さんも考えてみてください。

この問題のポイントは「分配法則」を使うということです。

今回は(a+b)(c+d)=a(c+d)+b(c+d)の形です。

このことを踏まえると、

（2－√6）（1+√6）=2（1+√6）－√6（1+√6）
=2+2√6－√6－6
=－4+√6

答えは、－4+√6　です。

皆さんは、解けましたか？分配法則さえ理解していれば解けたと思います。

このように実際の入試問題では「平方根」の分野は基本レベルの計算問題の出題が多いです。

しかし、油断してはいけません。「平方根」単独での問題は比較的簡単ですが、難易度が高い問題の中に「√」の数値がよく使われます。

そのため、難易度が高い問題で得点を取るためには「平方根」の計算の正確性が必須です。

手を抜かずにしっかりと勉強しましょう。

平方根の必勝法

ここまで平方根の性質や出題パターンを見てきましたが、実際に皆さんが自分の力で解き、高得点が取れなければ意味がありません。

そのため、今から「平方根」の必勝法をお伝えします。

平方根はひたすら「演習」です。出題傾向が単純な計算問題だからこそ1つも間違ってはいけません。

入試問題は「簡単な問題で満点を取り、難しい問題のカバーができるかどうか」が合格の分かれ道になります。

だからこそ平方根の単元では常に満点を取る必要があります。

そのために場数を踏むことと様々な種類の計算問題に出会うことが大切です。

演習を積むためにおすすめの参考書はこちらです。

『中学 数学 3年【基礎】問題集 2 平方根 DVD (授業+テキスト+問題集)”プロ家庭教師が教える”』

こちらはDVDを見ながら演習する形式なので、実力がつきます。ただ問題演習をするのではなく、耳と目からも知識を吸収できる一冊です。

また、先取学習をしたい中学1年生と2年生にもおすすめです。

丁寧な解説動画なので、平方根の知識がゼロの状態でも抵抗感なく勉強を始められます。

まとめ

ここまで平方根について一緒に勉強しましたが、いかがだったでしょうか？

平方根でいかに高得点を取れるかが高校入試の合否の分かれ目になりますので、ひとつひとつの問題を大切にしましょう。

そして平方根の分野を完璧にして自信を持って試験会場に向かいましょう！