高校入試の平面図形問題、でるのは3パターン！これさえ押さえてバッチリ

都立高校・私立高校を目指す受験生が、数学で苦手意識を抱えやすいのが「平面図形」。「相似・合同が見つけられない……」「どこの角度が同じかわからない……」といったことは多いのではないでしょうか。この記事では、そんな中学生に向けて、高校受験で出る「平面図形」問題の解き方のコツ・普段の勉強法をご紹介します。

高校入試の「平面図形」はこれだけ。苦手を特定しよう！

ひとことに「平面図形」といっても、様々な分野があります。点が取れない場合は「どの分野が取れていないのか？」「どの分野の基礎が抜けているのか？」をきちんと確認することが重要になります。ここから挙げる範囲の中で、少しでも「怪しいな……」という範囲があれば確認しておくようにしましょう。

• 作図
• 円・扇形と面積
• 角度（錯角・同位角）
• 三角形（合同・特徴）
• 四角形（平行四辺形・平行線の中の三角形の面積）
• 相似
• 円周角
• 三平方の定理

中学校での指導要領に沿って分けると上記の8つになります。意外と幅広くあるように感じますね。この中で単元を聞いて「あれ、この範囲怪しいな……」というところがあれば、まずはその範囲を完璧にするようにしましょう。

都立入試の平面図形は「第1問」「第4問」で組み合わせて出題

ただ、実際に出題される場合には、これらの範囲が単体で出題されることはあまりありません。例えば東京都の都立入試であれば、第1問のいわゆる「小問集合」というところで作図が単体で出題されることはありますが、他では角度の問題としてまとめて出題されたり、第4問で証明問題と角度問題をあわせて出されたりすることになります。

出典：都立入試2020年第1問（8）

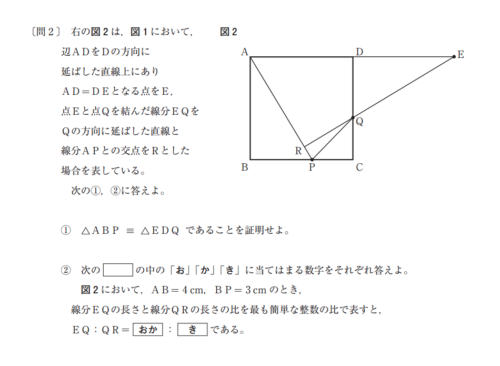
出典：都立入試2020年第4問

高校入試「平面図形」の出題3パターン！

このことから、入試で問われる「平面図形」は大きく3パターンに分けられます。この3つのパターンを徹底的に演習することが、高校入試の平面図形問題を攻略するカギになりますね。

平面図形のパターン1：「合同・相似の証明」＋「線分比」

1つ目のパターンは「合同・相似の図形を証明する」問題。都立入試では第4問の問2で出題されます。

四角形・三角形・円などを組み合わせた図形が出され、その中で指定された三角形の相似や合同を証明する問題、そして証明したあとでそれを使い線分比や線分の長さを問う問題が基本です。

場合によっては自分で補助線を引く必要があるため、ある程度似た問題を解いて正確に問題を把握するのはもちろん、解く方法も身につけておく必要があります。

証明はセオリー通り。必ず満点を取るべき！

一部の私立高校と違い、証明問題は穴埋め問題ではなく、最初の仮定と結論をきちんと読み取り、そこから証明をすべて書く必要があります。

その分配点も大きいのですが、実はこの証明問題はほぼパターンになっているため、他の問題と比べても絶対に落としたくない問題なんです。

他の計算問題などであれば計算ミスの可能性もありますが、証明問題の場合は「きちんと書ければOK」。もちろん細かいルールはありますが、それさえ覚えて書き慣れておくこと、そして条件をきちんと見つけることができれば間違えようがないんですね。そのうえ、計算問題や「長さ」「線分比」を求める問題と違いそこまで難易度が上がらないため、対策をしておけば確実に取れる問題だと言えるのです。

この証明で必ず取れるようになれば、点数が安定しきちんと合格点を狙えるようになりますから、どんな高校を受ける際も必ず満点をとるべき問題です。

証明の書き方や合同条件・相似条件は完璧に覚えるのが大前提ですが、一番悩むところとすれば「どこの角とどこの角が同じ大きさか？」など、条件にどこを使うかでしょう。基本的には

• 円周角が等しいこと
• 平行線の錯角・同位角が等しいこと
• 対頂角が等しいこと
• 平行四辺形・二等辺三角形など特殊な図形の性質を使うもの

に大まかに分類できます。これらに目をつけながら、「『1辺とその両端の角がそれぞれ等しい』を使うにはあとここが同じかも？」「こことここが同じなら『3辺がそれぞれ等しい』になるからなにか条件が隠れてないかな」というふうに条件を当てはめながら探していくことになります。最後に改めて条件に間違いがないか（2辺とその間の角ではなく角の場所がずれてしまっていないか？など）に注意して、しっかり丁寧に書ききりましょう。

線分比・長さの問題は「図を描き直す」のがコツ

証明問題のあとに必ず出る問題が、線分比や面積比、線分の長さを問う問題。これが平面図形の問題でも最難となっています。

パターンとしては基本的に、事前にもとめた相似や合同を使って

• 線分の比を求めさせる
• 面積比（何倍か？）を求める
• 線分の長さを求める

の3つに分けられます。証明問題に比べると難易度が高いため、あまり高得点を狙わないのであればある程度捨ててもOKです。平面図形の問題でこのような「値を求める」問題になると、「気づかないと解けない、というループにハマってしまう」ことが多々あるため、ある程度考えて厳しそうであれば飛ばして他の問題で点をとっていく、という戦略も必要です。

 

ただ、高得点が必要な場合はこの問題も必ず取るべきところです。特に都立の独自校や私立難関高校を受験する場合はここで差がつくと言っても過言ではありません。

 

こうした難しい平面図形の値を求める問題をクリアするためのポイントはよく「補助線」だと言われますが、実はそれだけでは不十分。ここではもっと丁寧に「図を描き直す」というところからコツとして大事なんです。

というのも、入試問題にもともとついている図は「小さい」うえ「たまに不正確なことがある」から。不正確な、しかも小さい図に補助線を引いたとしても、角の大きさが実際と違いすぎてなかなか気づきづらいのはもちろん、間違って線を引いたりぐちゃぐちゃになったりしてしまいます。

必ず余白にこれでもかというくらい大きく、かつざっくり求めた値や相似・合同を条件通りに描きなおしてから、そこに線を引いたり値を実際に埋めていったりすることで、正答に近づくことができます。図を条件通りに、かつフリーハンドで（本番定規で描く時間はありませんから）描く練習を問題を解くたびにしておきましょう。

平面図形のパターン2：「角度問題」

 

第1問の小問集合では「角度問題」「作図」の2つがよく出題されます。

「角度問題」とはこのような、円周角や平行線などを駆使して角の大きさを求める問題。都立入試だとここ数年はほとんど円周角の問題が出されています。

出典：都立入試2020年第1問（8）

基本に忠実に解けば解ける問題ばかりです。

解くコツは「平行線を作る」「円周角を見間違えない」こと

都立の円周角問題は基本的な問題ですから、「円周角でない部分を見間違えない」など初歩的なミスを防いでいけば十分時間をかけずに解答することが可能です。焦っていると以下のようなものでも見間違えてしまう事があるので要注意です。

 

 

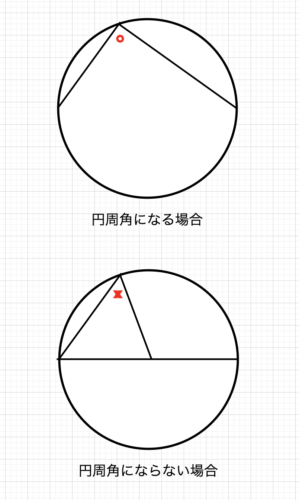
平行線や三角形を使った角度の問題は独自校や難関私立で出されますが、ポイントは「平行線を作る」こと。

折れ目が多い図形ほど、平行線を作って角度を分解することが重要になります。これができれば平行線の同位角・錯角を使って角度を求められますので、このあたりをきちんと意識して補助線を適切に引けるようになりましょう。

 

平面図形のパターン3：「作図」

 

都立で必ず出題される作図問題も、基本的には教科書レベル。

• 角の二等分線
• 垂直二等分線

がよく問われます。気をつけるべきなのは「垂直二等分線を書きなさい」という出題ではなく「辺AC上にあり、AP＝BPとなる点Pを書きなさい」のように出されること。このときに一発で「線分ABの垂直二等分線上の点Pは必ずAP＝BPになるから、垂直二等分線とACの交点がPになればいいな」と変換できるかがポイントです。作図のやり方自体は絶対に押さえておく大前提として、「どういう作図をしないといけないのか」をきちんと読み取るようにします。

問題文からどういう作図か読み取るコツ

問題文から「この場合は垂直二等分線」などと読み解くコツは、「作図することでできること」をきちんと知ることです。

例えば

• ある線分ABの垂直二等分線を引いたら、その垂直二等分線上にある点PはどこであってもAP=BPになる
• コンパスの針を点Aにおいて印をつけた点BとCについては、AB=ACが成り立つ

など。円を描いているんだから当たり前じゃん！と思える人はすでにできているので、ミスをしないようにだけ気をつけましょう。「なにこれ？」という人は、コンパスの作図でなぜこういう図形が書けるのか？を考えておくと、こうした問題文からの変換がやりやすくなります。

平面図形の3パターンを直前でイッキに引き上げるコツ3つ

平面図形の3パターンは

• 作図
• 角度
• 証明

でした。「今から対策したいんだけど間に合うかな？」という直前期の人は、とりあえず次のことを押さえましょう！

合同条件・相似条件をとにかく覚える

まずは証明できちんと点が取れるようになるべきなので、証明問題で必ず問われる「合同条件」「相似条件」を正確に書けるようになっておきましょう。それぞれ3つずつしか無いので、きちんと覚えておけば書けるはずですよね。

合同条件・相似条件を覚えるポイントは、「なんども唱える」ことと「一言一句間違えないように覚える」ことです。「それぞれ」「両端」などの言葉にも大事な意味がありますから、必ず丸覚えして、それぞれどういう状態なのかを確認しておきましょう。

合同条件3つ

• 3辺がそれぞれ等しい
• 2辺とその間の角がそれぞれ等しい
• 1辺とその両端の角がそれぞれ等しい

相似条件3つ

• 2組の角がそれぞれ等しい
• 2組の辺の比が等しく、その間の角が等しい
• 3組の辺の比がすべて等しい

合同・相似条件が隠れているパターンを覚える

次に押さえるべきなのは、よく出る「合同条件の見つけ方」「相似条件の見つけ方」です。以下の要素をよく見て、「角が同じだな」「辺の長さが同じだな」というのを確認していきます。

合同

• 平行線の錯角と対頂角
• 平行四辺形の辺の長さと対角

相似

• 三角形の中に1本線が引いてあり、共通角と辺の長さの比（もしくは平行線の同位角）を使う
• おなじ弧に対する円周角をなす直線で三角形を作る

これらの「目の付け所」がきちんと把握できているだけで、証明するときに条件を見つけやすくなります。

円周角の問題をたくさん解いておく

円周角については、問題をたくさん解いて「どこの角とどこの角が同じ」というものをパッと見ただけで見極められるようになっておきましょう。

慣れていないと円周角でないところなのに円周角だと捉えてしまうことがあります。

円周角の問題は絶対に落とせない問題ですから、確実に取るために問題演習を重ねておきましょう。

まとめ

平面図形はきちんと対策さえすれば確実に加点できる分野です。苦手な人も「ここだけ押さえればOK」というところだけでも確実に点を取るようにしましょう。