高校入試対策！数学の「錯角」をバッチリ理解するコツを徹底解説！

同位角と錯角は平行線の性質を表すときにも登場します。

その際、どちらも似たような性質を持っているので混同してしまいやすいです。

この記事を読んで、同位角と錯角の区別がしっかり付けられるようになりましょう！

なお同位角について詳しく解説した記事もありますので、ぜひそちらも読んでみてくださいね。

錯角とは

2直線l, mに直線nが交わっているとき、∠cと∠eのような位置にある2つの角を錯角といいます。

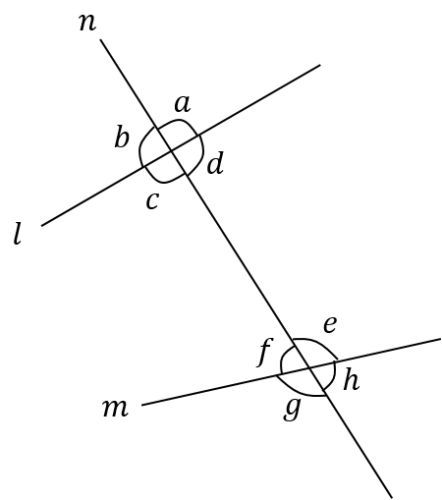
このように2直線l, mに直線nが交わっているとき、錯角には全部で2つの組合せがあります。

上図において、他に錯角の関係にあるのは∠dと∠fです。

ちなみに漢字表記は錯「角」です。

「目の錯覚」などというときに使う錯「覚」とは異なるので注意しましょう。

錯角を理解するポイント！

図の中にある錯角を探す前に、錯角の定義の文章を読み返してみましょう。

「2直線l, mに直線nが交わっているとき、∠cと∠eのような位置にある2つの角を錯角といいます。」

この文章をよく読むと、錯角とは「2つの角」を指すことがわかります。

図を見て「錯角はどれって言われても……」と、1つの角を探していませんか？

どことどこが錯角の関係にあるか考える時には、必ず「2つの角」をセットで考えましょう。

いろんな錯角の見つけ方

さて、それでは錯角の見つけ方・覚え方を3つご紹介しましょう。

• Zを探せ！
  
• 回転させて見てみる！
  
• 3つの領域に分けて考えてみる！

重要なのは「どうやって見つけるか」ではなく「間違いなく見つけること」です。

どの方法でも構いませんので、自分が一番わかりやすいと思う方法で錯角の位置関係を頭に入れてください！

Zを探せ！

先ほどの図を、錯角を示すのに必要な部分だけに注目して見てみましょう。

錯角の周りだけ示そうと思うと、Zの形が浮かび上がってきますね。

「錯角はZAっと見てZを探せ！」と覚えてみてください。

回転させて見てみる！

直線同士によって分けられた領域を、時計回りに右上・右下・左下・左上と考えるのも1つの手です。

でもこのとき、直線がすべて斜めに引かれていると「どこが右上？ここは右上じゃなくて右下？」というように迷うことがあります。

この迷いがミスにつながりやすいので要注意！

こういうときは、2直線を貫いている直線（図で言えば直線n）を縦でも横でもいいのでまっすぐにしてみましょう。

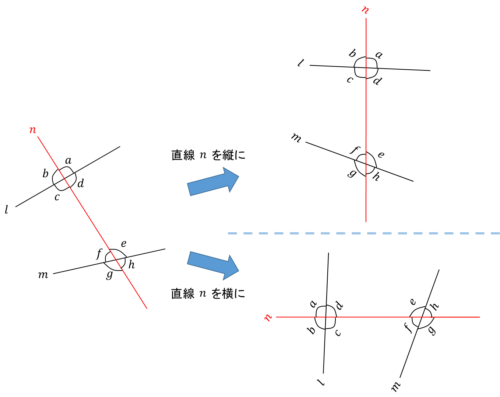
途端に位置関係がわかりやすくなりませんか？

直線が全て斜めでややこしいな～～と感じたら、どれか1つをまっすぐにしてみてください。

3つの領域に分けて考えてみる！

他にもこんな考え方があります。

2直線l, mに直線nが交わっているとき、2直線l, mによって3つの領域に分かれていると考えてみましょう。

こう考えると、錯角はいずれも真ん中の領域にあることが見えてきます。

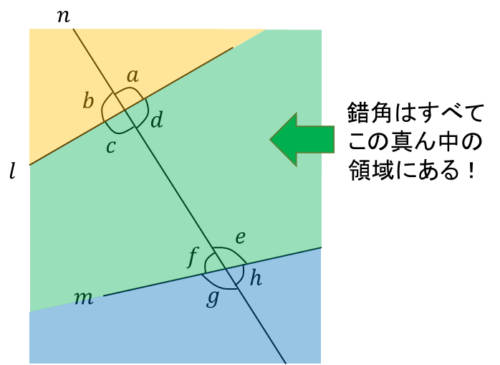
両サイドの外側に開けた領域には錯角がないことを押さえておきましょう。

錯角に関する重要な性質

さて、いろんな錯角の見つけ方をご紹介してきましたがいかがでしたでしょうか？

いろんな考え方に触れたことで錯角を見つけるのが速くなってきたら、錯角という言葉を活用する段階に進んでみましょう。

ここでは錯角に関する重要な性質を2つ挙げます。

• 2直線に1つの直線が交わるとき、2直線が平行ならば錯角は等しい。
  
• 2直線に1つの直線が交わるとき、錯角が等しければこの2直線は平行になる。

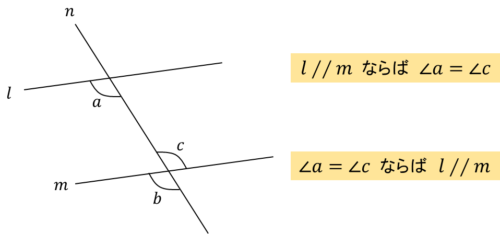
このような平行線と錯角の関係は、平行線と同位角の関係から説明することができます。

証明問題が問われることもあるので、説明の流れはきちんと追えるようにしておきましょう。

平行線と同位角＆錯角の性質

これまでに、平行線と関係のある3つの角、対頂角・同位角・錯角のすべてを学んできました。

ここでまとめとして、平行線と同位角＆錯角の性質を復習しておきましょう。

• 2直線に1つの直線が交わるとき、2直線が平行ならば同位角は等しい。
• 2直線に1つの直線が交わるとき、2直線が平行ならば錯角は等しい。
• 2直線に1つの直線が交わるとき、同位角が等しければこの2直線は平行になる。
• 2直線に1つの直線が交わるとき、錯角が等しければこの2直線は平行になる。

もちろん、これらの性質からも「対頂角は等しい」ことが確認できますね。

対頂角・同位角・錯角と平行線との関係性は図形問題に必須の知識なので、図を見てパッと答えられるように練習しておきましょう。

錯角の問題を解いてみよう

それでは、この性質を問題でどう活かすのか、実際の入試問題を解きながら見てみましょう。

以下の問題は、平成30年度都立高校入試大問1の問8です。

“次の図で l // m のとき、xで示した角の大きさを求めよ。”

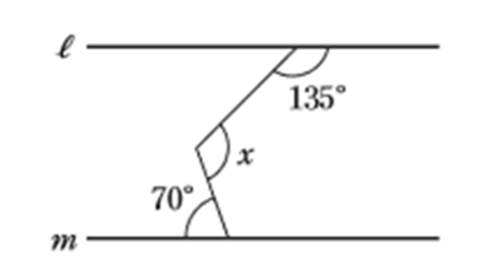
では、早速解いていきましょう。

錯角と平行線の関係を使って角xを求めるために、まず角xの部分に、直線l, mに平行な補助線を引きましょう。

この補助線は直線mと平行なので、上図の赤色で示した角の大きさが70°だとわかります。

次に、この補助線と直線lも平行なので、下図のとおり錯角は等しくなります。

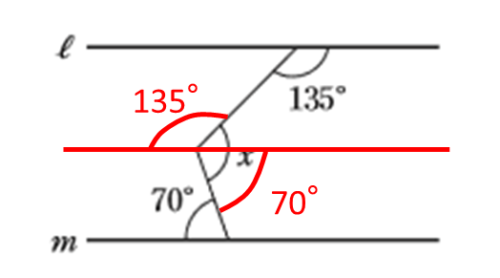
すると、角xのわかっていなかった部分は次のように値が求められます。

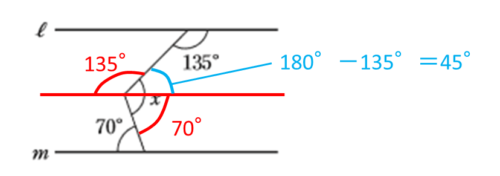
よって、角xの大きさは45°＋70°＝115°です。

錯角の勉強方法

問題の感覚がつかめたところで、勉強方法をまとめましょう。

自分なりの見つけ方をしっかり覚えよう

この記事でいくつか錯角の見つけ方をご紹介しましたが、その全てを覚える必要はありません。

自分が一番わかりやすいと思ったもの1つで良いので、その1つを完璧に覚えましょう。

とにかく数をこなそう

錯角を間違いなく見つけるためには、図を見てパッと答えられるくらいまで目を慣らすことが大切です。

「錯角の問題に関しては、一目見ただけでスラスラ解けるようになった」と言えるくらいまで練習問題をこなすのが良いでしょう。

錯角の直前対策法！

それでは具体的に、錯角の直前対策としてどのようなことに取り組めば良いのでしょうか？

都立高校入試では図形問題は頻出です。

また大問として出題されることもあります。

その問題を解くための武器の1つとして錯角の性質を使えるよう、次のことを意識してみましょう。

錯角と平行線・対頂角・同位角の関係を押さえる

錯角と平行線の関係性を使うような場面では、対頂角や同位角といった知識も一緒に使うことが多いです。

• 対頂角はいつでも等しい
  
• 同位角は2直線が平行ならば等しい
  
• 錯角は2直線が平行ならば等しい

これらはセットで頭に入れておき、いつでも知識を使えるようにしておきましょう。

錯角を作り出すための補助線の引き方を覚える

先ほど解説した過去問のように、一見しただけでは錯角が見つからない図が出題されることもあります。

こういった問題に当たったときは、どこに補助線を引けば錯角や同位角の知識を活用できるかを考えてみましょう。

まとめ

錯角のいろんな見つけ方から入試問題での知識の活かし方までご説明してきましたが、いかがでしたでしょうか？

自分なりの見つけ方を一度習得できれば忘れないので、練習問題をたくさん解いて「自分のモノ」にしてくださいね。

図形問題の基礎知識として、錯角への苦手意識は早めになくしておきましょう！