中学3年間でたくさんの図形の知識を勉強します。
その中でも「三平方の定理」は中学3年生で勉強するため高校入試までに復習する時間が比較的とれない単元です。
そのため「よくわからないまま高校入試当日を迎えてしまった」という高校受験生も多いです。
そうならないように今回は三平方の定理の受験必勝法について詳しくお伝えします。
三平方の定理とは?
「三平方の定理とは何ですか?」という質問に皆さんはパッと的確に答えることはできますか?
できないようでしたら、今ここで一緒に確認しましょう。
三平方の定理とはひとことでまとめると「直角三角形の3辺の長さの関係を表す公式」です。

上記のような公式が成り立ちます。直角三角形においてcを斜辺とします。すると、斜辺以外の2辺を2乗した数の和に等しいという公式です。
「どうやって斜辺を見分けるの?」と思う方がいると思います。斜辺は直角三角形の3辺の中で一番長い辺と覚えれば大丈夫です。
このことより、直角三角形において2辺の長さがわかっていると残り1辺の長さを求めることができます。
続いて三平方の定理の重要ポイントを見てみましょう。
三平方の定理重要ポイント
三平方の定理の中でも絶対に覚えてほしいポイントが3点あります。
「30°×60°×90°の直角三角形」の辺の比

三角定規でもお馴染みの「30°×60°×90°の直角三角形」の辺の比は「1:2;√3」です。この数字はよく出てくるのでしっかりと覚えましょう。
「45°×45°×90°の直角三角形」の辺の比

またこちらも三角定規でもお馴染みの「45°×45°×90°の直角三角形」の辺の比は「1:1;√2」です。この数字はよく出てくるのでしっかりと覚えましょう。
「30°×60°×90°の直角三角形」と「45°×45°×90°の直角三角形」の辺の比はただ覚えているだけではいけません。なぜならこの図形だけで辺の比を求めなければならない問題は少ないためです。
一般的には、図形が複雑に絡み合いその中で自分の力でこの2つの図形を見つけ出す問題が多いです。
そのため、この角度の数字が出てきたら「もしかしたらこの辺の比を使って解くのかもしれない…!」とアンテナを張りましょう。
三平方の定理の逆
「三平方の定理の逆」というものがあります。これは文字通り三平方の定理の逆が成り立つのです。
これによって、三角形の「a²+b²=c²」が成り立てばその三角形は「直角三角形」であるということがわかります。
さらに三角形の比が「1:2;√3」であったら「30°×60°×90°の直角三角形」、「1:1;√2」であったら「45°×45°×90°の直角三角形」であることがわかります。
このような法則がすぐ頭の中に浮かぶように、これらの重要ポイントをしっかりおさえましょう。
三平方の定理出題傾向
ここまで三平方の定理を見てきましたが、どのような出題傾向があるのでしょうか?
今回は都立高校の実際の入試問題の内容を抜粋しましたので、一緒に考えてみましょう。
こちらの問題は都立高校入試の平成29年度の大問4です。

“”上記の図で四角形ABCDは、AB=6㎝、BC=12㎝の長方形である。
辺BCを直径とする半円Oの弧BCは2つの頂点B、Cを通る直線に対して頂点Aを同じ側にある。
点Pは、辺AD上にある点で、頂点Aに一致しない。
頂点Bと点Pを結んだ線分と、弧BCとの交点のうち、頂点Bと異なる点をQとする。
また、△ABPと△QCBは相似の関係にある。
AP:PD=1:3のとき、線分PQの長さは□㎝である。
□にあてはまる数字を答えなさい。“”
では早速解いていきましょう。
線分PQの長さを求めなければなりません。
図から読み取って「線分PQ=線分PBー線分QB」で求められると判断します。
つまり、線分PBと線分QBの長さを求めることができたら答えは出せます。
そこで相似の関係にある△ABPと△QCBを利用します。

AP:PD=1:3、AD=12㎝より
AP=3㎝であることがわかります。
また問題文よりAB=6㎝なので
「三平方の定理」により
BP²=AP²+AB²
BP²=9+36=45
BP=3√5
このことにより△ABPは「3㎝、6㎝、3√5㎝」であり「1:2:√5」の直角三角形ということがわかります。
数値をまとめると以下のようになります。

求めたい線分BPと線分BQを赤で示しました。
相似のためどちらも同じ「1:2:√5」の比になります。
まだ数値がわかっていない線分BQをXと置きます。
このことを踏まえて式をたてると
3:3√5=X:12(1:√5=X:12でもOKです)になります。
これを解くと
3√5×X=3×12
X=12/√5=12√5/5
BQ=12√5/5
を求めることができました。
BP‐BQ=PQなので
3√5‐12√5/5=3√5/5=PQ
答えは
3√5/5㎝です!
お疲れ様でした!いかがでしたでしょうか?都立高校の実際の入試問題でも「三平方の定理」が大活躍します。
またこの問題のように「三角形の相似」の問題との融合問題が多いので、相似についてもしっかりと勉強してください。
三平方の定理で高得点を取る必勝法
ここまで詳しく見てきましたが、良い点数を取らなければ意味はありません。
ではどのようにして三平方の定理を得意にして高得点を取る事ができるのでしょうか?
そのためには様々な出題傾向に慣れる事が非常に重要です。
実際の高校入試で三平方の定理は、わかりやすい直角三角形の姿で出題されることは滅多にありません。
複雑な図形の中から直角三角形を見つけ出して数値を求めることがメインです。
例としてこのような形があります。
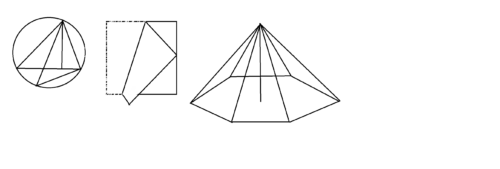
このような複雑な図形の中から見つけ出します。
ではどのようにして見つけ出すのでしょうか?
それは「場数」です。多くの演習量を積んでたくさんの種類の図形に出会いましょう。
解いていくうちにだんだんとスピード感を持って直角三角形を見つけ出して三平方の定理を使うことができます。
三平方の定理おすすめ参考書
その場数を踏むためにおすすめの参考書はこちらです。
『ひとりで学べる数学教材【中学数学】三平方の定理【自立学習教材・反転授業副教材】』
楽天市場で購入できますので調べてみてください。
こちらは対象学年が中学1年生からとなっています。三平方の定理は中学3年生の最後に学校で教わる単元なので、高校入試までに間に合わない受験生も多いです。
そのため三平方の定理は「どれだけ早い時期から勉強したか」が勝負になります。
そのため、中学1年生と2年生はこの参考書で先取学習して他の受験生と差を付けましょう。
三平方の定理にまだ苦手意識のある中学3年生はこの参考書で苦手克服に努めましょう。
まとめ
「三平方の定理」は「中学数学の最後にして最大の壁」と言われています。そのため、いかに早い時期から勉強するかが合格の分かれ目となります。
複雑な図形が絡み合って出題されますが、あくまでベースは基本的な「三平方の定理」というルールです。焦らずに基本に忠実に解きましょう。














