中学理科「圧力」を理解しよう！イメージがつかめる勉強法

「圧力ってなに？力という字が付いているから、力と同じじゃないの？」

そう考えてしまってイメージしづらいのが、この記事で学ぶ「圧力」です。

目に見えないものだからこそ、「力」と「圧力」がどう違うのかしっかり区別できるようにポイントを整理していきましょう！

圧力とは

圧力とは「一定の面積にはたらく力」のこと。

「結局力なの？」と思われるかもしれませんが、力との関係は次の式で表されるため厳密には少し異なります。

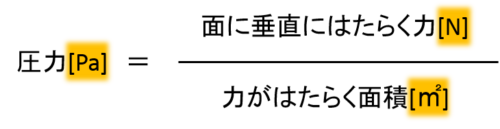
このように力は力でも面積あたりの力なので、力は[N]、圧力は[Pa]と単位が異なることがポイントです。

圧力を理解することがなぜ大切か

「でも結局力の話になるんだったら、圧力なんて使わなくてもいいんじゃないの？」

そんなもやもやを残さないために、圧力を理解すべき理由からお伝えしましょう。

高校入試では圧力そのものを求める問題も出題されますが、圧力という考え方を使った浮力や気圧の問題が出されることもあります。

さらに大問で出ることが多い力や運動の分野で、圧力から力を求めてその後の設問で求めた値を使うなんてケースもあります。

その場合、途中の設問で間違えるとその後の配点も取れないなんてことになってしまいます。

そんな事態にならないために、圧力と力を結びつけて考えられるようになっておく必要があります。

「結局力の話になる」のではなく「圧力が出てきても力の話に持ち込める」と考えて、しっかり理解しておきましょう。

圧力を理解する上で覚えておきたいポイント！

なんとなく力との違いがわかってきたでしょうか？

ここからは、圧力とは何かを理解するために押さえておきたいポイントをご紹介します。

ポイント①面積によって力のはたらき方は違う

まず、なぜ「面積当たりの力」を考える必要があるのかお伝えします。

それは、力がはたらく面積によって力のはたらき方が違うからです。

具体的なもので考えてみましょう。手元にあるシャーペンの、ノックする側で手のひらを押してみてください。別に痛くないですよね。

では同じ力で、今度は芯の出る側で手のひらを押してみてください。「痛そうでそんなことできない！」と思いませんでしたか？

そう直感できているなら、もう圧力のことは理解できています。

同じ力を加えるのに、どうして力のはたらき方が違うのか。

それはシャーペンの両端で面積が違うからです。

鞄の紐が細いとなぜ荷物が重く感じるのか、包丁は少しの力でなぜ食材を切れるのか、そういったことも圧力で説明ができます。

ポイント②力と圧力の関係を押さえる

改めて力と圧力の関係式を見てみましょう。

[Pa]はパスカル、[N]はニュートン、[㎡]は平方メートルと読みます。

同じ力でも、力がはたらく面積が小さいほど圧力は大きくなります。

同じ面積なら、力が大きいほど圧力も大きくなります。

ポイント③「力→圧力」「圧力→力」を求められるようにする

先ほどの関係式から、[Pa]＝[N/㎡]、[N]＝[Pa×㎡]と表せることがわかります。

力から圧力、圧力から力、どちらの変換もスムーズにできるようによく練習しておきましょう。

ここで注意したい点が2つあります。

面に垂直にはたらく力であること

下の図のように、はたらく力の向きと力のはたらく面が垂直でない場合があります。

この場合、斜面と接している面にかかる圧力は、面に垂直にはたらく力と面に平行にはたらく力に分解してから考えるようにしましょう。

面積の単位が[㎡]であること

先ほどの関係式において、面積の単位が[㎡]であることに気をつけましょう。

問題文には、物体の大きさを表すのに[cm]や[mm]が使われていることがあります。

単位の換算を忘れてケアレスミス…なんてもったいないので、注意が必要です。

単位換算はいつ行ってもいいですが、計算し始める前、長さを書き出すタイミングで行うのがおすすめです。

なぜなら、計算の最後に換算しようと考えていると、数値を見て安心してしまって換算し忘れる可能性が高いからです。

最初に単位換算する習慣をつけましょう。

実際にどのような問題が出題されるのか？

それでは実際の入試問題を解いてみましょう。

以下の問題は、平成26年度都立高校入試の大問2から抜粋したものです。

”＜レポート2＞集中豪雨による浸水被害について
短時間に大量の雨が降り、雨水を処理しきれなくなると、下水道管から水が地表にあふれ出し、地下室等の低いところに流入し、浸水することがある。
ドアの外側の水位が約30cmになると、水圧によって外開きのドアは開かなくなる可能性が高くなることから、雨の多い季節や地域では、地下への浸水対策が必要である。
水圧は水の深さと関係があり、水位が30cmのときは、ドアの水につかっている面にかかる圧力は平均すると、1500Pa（N/㎡）であることが分かった。

＜レポート2＞から、水位が30cmのとき、幅が90cmのドアが水から受ける力の大きさとして適切なのは、次のうちではどれか。

ア：50N、イ：405N、ウ：45000N、エ：4050000N”

では、早速解いていきましょう。

水位が30cmのとき、幅が90cmのドアが水から力を受けている面積は0.27㎡です。

ドアの水につかっている面にかかる圧力は1500Pa（N/㎡）なので、ドアが水から受ける力の大きさは

面に垂直にはたらく力[N] ＝圧力[Pa]×力がはたらく面積[㎡] ＝1500Pa×0.27㎡
＝405N

よって、正解はイ：405Nです。

圧力の勉強方法について

問題の感覚がつかめたところで、勉強方法をまとめましょう。

面積を変えるとどうなるかイメージする！

何度も見てきた力と圧力の関係式を眺めながら、力のはたらく面積を変えたときの力と圧力の関係をイメージできるようにするのが大切です。

力の大きさが同じとき、力がはたらく面積が1/2になれば圧力は2倍に。

同じ面積なら、力が2倍になれば圧力も2倍です。

では、面積が2倍になっても圧力が変わらない場合、力の大きさはどうなっているでしょう？

力の大きさも2倍になっています。

このように力、圧力、面積をそれぞれ変えたらどうなるかを考えてみて、圧力というものをイメージできるようにしておきましょう。

この後の単元では、水圧と浮力、気圧といった「目に見えないもの」を理解することが求められます。

ここで圧力という概念をしっかりイメージできれば、この後の勉強もスムーズに進みます。

圧力の直前対策法！

それでは具体的に、圧力の直前対策としてどのようなことに取り組めば良いのでしょうか？

他の単元と組み合わせて解けるようにする！

入試問題に圧力単体で出題されることは少なく、たいてい力のつり合いや物体の運動など、他の単元と組み合わせて出題されます。

前述した、水圧と浮力や気圧の問題と絡めて出題されることもあります。

そのため、自分に合った問題集などで組み合わされている設問に取り組み、様々なパターンに慣れておきましょう。

「力」と「圧力」の違いを覚える！

上記のように問題に取り組む際に「力」と混同してしまわないよう、

• 力は[N]
• 圧力は[Pa]＝[N/㎡]

という「力」と「圧力」の単位の違いをきちんと押さえておきましょう。

単位間違いに注意！

ポイント③でも触れましたが、圧力の関係式における面積の単位は[㎡]です。

でも、問題文には長さが[cm]や[mm]で書かれていることも多いです。

もしも先ほどの過去問でcmをmに直し忘れて計算してしまうと、

面に垂直にはたらく力
＝圧力×力がはたらく面積
＝1500Pa×30cm×90cm
＝4050000

となり、数字だけ見てエが正解だ！と思い込み、間違えてしまうことになります。

選択肢には計算ミスで選びやすい誤答が並んでいることも多いので、単位の換算ミスには十分に注意しましょう。

最後に単位換算しようと考えていると、数字を見て安心して単位換算を忘れてしまうこともあり得ます。

解き方で示したように、計算し始める前に単位を揃えることを習慣化しましょう。

まとめ

圧力と力の違いがばっちり理解できたでしょうか？

ここで確実に理解しておくと、その後の学習もスムーズになります。

圧力というものをしっかりイメージできるようにしておきましょう！