仕事という言葉にはいろいろな意味がありますね。
会社員や医者など「職業」という意味や、「学生の仕事は勉強」のような「やるべきこと」という意味などがあります。
では、理科における「仕事」とはどんな意味なのでしょうか。
この記事では「仕事」とはなにかというところから入試での出題傾向までしっかりお伝えしていきます。
仕事とは
理科では、「力を加えて物体を動かしたときの作業量」を仕事といいます。
具体的には「物体が力を加えた方向に動いたとき、力が物体に対して仕事をした」といいます。
仕事の大きさは、「物体に力を加えて物体を動かしたときの力の大きさ」と「力の向きに動かした距離」との「積」で表します。
![]()
仕事の単位はジュールと読みます。
物体を1Nの力で力の向きに1m動かしたときの仕事が1Jです。
仕事を理解する上で覚えておきたいポイント!
仕事の概要がつかめたところで、ここからは仕事を理解するために押さえておきたいポイントをご紹介します。
- ポイント①仕事の大きさは「力の大きさ」と「距離」で決まる!
- ポイント②力の向きと動かした向きが大切!
- ポイント③仕事の原理を覚えよう
- ポイント④仕事率を理解しよう
では、順番に見ていきましょう。
ポイント①仕事の大きさは「力の大きさ」と「距離」で決まる!
次のような場合について仕事の大きさを考えてみましょう。
図の中で、青い箱ひとつの質量は1kgであるとします。
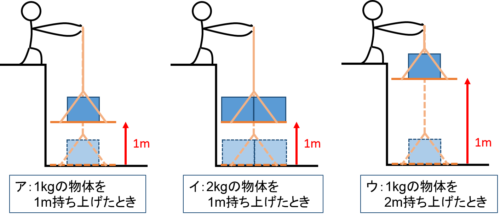
ここでア、イ、ウそれぞれの仕事の大きさは何Jでしょうか?
なんとなく「ア<イ、ア<ウかなぁ」と予想できるかもしれませんが、イとウではどうでしょうか?
力の大きさが変わると仕事の大きさも変わる
100gの物体にはたらく重力の大きさが1Nなので、1kgの物体を持ち上げるのに必要な力は10Nですね。
アとイでは、どちらも1m持ち上げているので、仕事の大きさは
ア:10N×1m=10J
イ:20N×1m=20J
となります。このように動かす距離が同じでも、力の大きさが変わると仕事の大きさは変わります。
動かした距離が変わっても仕事の大きさは変わる
では、物体の質量が同じで動かした距離が違うアとウではどうでしょうか。
仕事の大きさは
ア:10N×1m=10J
ウ:10N×2m=20J
となります。このように力の大きさが同じでも、動かした距離が変わると仕事の大きさは変わります。
そして、力の大きさも動かした距離も違って見えたイとウの仕事の大きさは、同じだったのです。
ポイント②力の向きと動かした向きが大切!
ここでもう一度、仕事を表す式をよく見てみましょう。
![]()
「力の向きに」という言葉がありますね。
実はこの言葉がとても重要です。
2つの向きが一緒かどうか確かめよう
次の図のような力を加えて、物体を斜面に沿って動かしたとしましょう。

この場合、物体が動いた向きも図に描き加えると次のようになります。
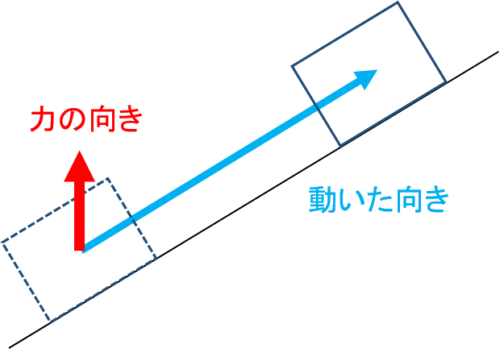
力の向きと動かした距離は違っていますね。
このような場合に仕事の大きさを考えようと思うと、赤い矢印で示した「力の大きさ」と「力の向きに動かした距離」が必要です。
この場合「力の向きに動かした距離」は次のようになります。
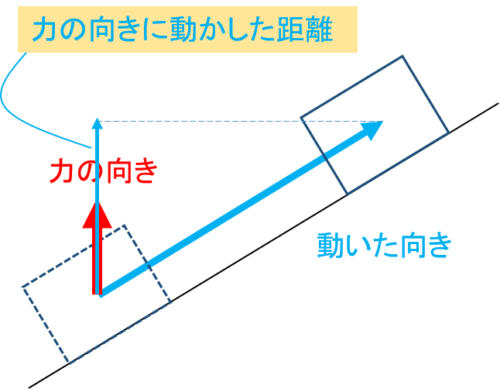
うっかり「物体が斜面上を動いた距離」で計算してしまうと間違った答えになってしまうので、力の向きと動かした向きが一緒かどうかはよく確認しましょう!
力がはたらいているのに仕事がゼロになることもある!
このように力の向きと動かした向きを考えたとき、極端な例では「力がはたらいているのに仕事の大きさが0」になることがあります。
- 荷物を持っているだけで動かした距離が0のとき
- 荷物を持ってゆっくり移動したとき(移動する向きの力は0)
- 強い力で壁を押したけれど動かなかったとき
こういった例は、いずれも仕事の大きさが0です。
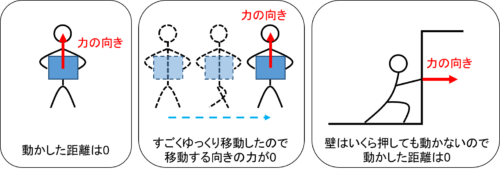
いずれもイメージすると大変そうですよね。
でも、理科的に考えると仕事の大きさは0になります。
なんとなくのイメージで考えるのではなく、力の向きと動かした向きをきちんと確かめましょう。
ポイント③仕事の原理を覚えよう
同じ大きさの仕事をするなら、できるだけ小さな力で物体を動かしたいですよね。
それを実現するために斜面や滑車、てこといった工夫が考え出されました。
例えば山の頂上まで登りたいとき、距離は短い断崖絶壁と距離は長いけれどゆるやかな斜面だったら、後者を選びますよね。
このイメージで1mの高さまで物体を持ち上げるときの仕事の大きさを考えてみましょう。
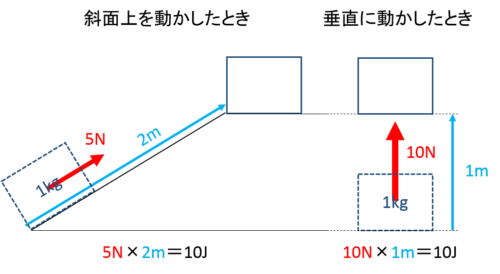
実は、どちらも仕事の大きさは一緒です。
これを「仕事の原理」といいます。
斜面を使うと動かす距離は大きくなりますが、必要な力は小さくなることに注目しましょう。
ちなみになぜ仕事の原理が成り立つかは、このあとの単元で習う位置エネルギーで説明できます。
気になった方は、ぜひあとで考えてみてくださいね。
ポイント④仕事率を理解しよう
先ほどの登山の例で、仕事の大きさは同じと言っても断崖絶壁を登るのとゆるやかな登山道ではかかる時間も違いそうだな、と思いませんか?
そう、やるからには効率良く仕事をしたいですよね。
そこで登場するのが「仕事率」という考え方です。
仕事率は、以下の式で表されます。

仕事率の単位は「ワット」と読みます。
ここで「聞き覚えがあるなぁ」と思った方は記憶力が良いです!
実は仕事率の単位ワット(W)も仕事の単位ジュール(J)も、すでに習っているのです。
電力量と、1sあたりのエネルギーを表す電力[W]という考えと同じだと理解しましょう。
実際にどのような問題が出題されるのか?
それでは実際の入試問題を解いてみましょう。
以下の問題は、平成30年度都立高校入試の大問2から抜粋したものです。
“<レポート1>仕事の大きさと仕事率について
ケーブルカーで山頂の駅まで移動し休憩所に着いた。休憩所の管理人から、ケーブルカーの開通以前は、飲み物などの荷物を人が背負って徒歩で運んでいたことを聞いた。そこで、ケーブルカーを利用して荷物を運ぶ場合と徒歩で荷物を運ぶ場合の仕事の大きさと仕事率について調べることにした。
麓の駅から山頂の駅までの区間では、標高差が450mある。この区間の所要時間は、ケーブルカーを利用すると5分であり、徒歩で登ると50分であることが分かった。
<レポート1>から、質量5kgの荷物を麓の駅から山頂の駅まで運ぶとき、ケーブルカーを利用したときと徒歩のときの、仕事の大きさの関係について述べたものと、仕事率の関係について述べたものを組み合わせたものとして適切なのは、次の表のア~エのうちではどれか。”

では、早速解いていきましょう。
標高差や質量の値が書かれていますが、この値がどうであれ、仕事の原理からケーブルカーを使った場合も徒歩で運んだ場合も仕事の大きさは一緒です。
よって、選択肢はウかエに絞られます。
続いて、仕事率の式を思い出してみましょう。
仕事率[W]は、仕事の大きさ[J]を時間[s]で割ったものでしたね。
5kgの荷物にはたらく重力の大きさは50Nなので、仕事の大きさはいずれも50N×450m=22500Jです。
仕事率は、ケーブルカーを利用した場合は5分=300sかかるので、22500J÷300s=75Wです。
徒歩の場合は50分=3000sかかるので、22500J÷3000s=7.5Wです。
よって、仕事率はケーブルカーを利用した方が10倍大きく、答えはエとなります。
この問題、実は仕事の大きさや仕事率の大きさを具体的に計算しなくても解けることにお気付きでしょうか?
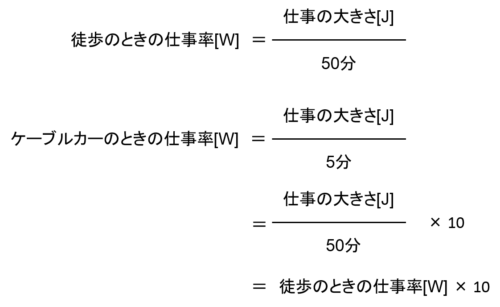
このように「仕事の大きさが同じでかかる時間が10倍違う」ということさえ気が付けば、具体的な大きさを求めなくても解けるのです。
問題にかける時間を短縮するために、こういったテクニックがあることもできれば頭の片隅においておきましょう。
仕事の勉強方法について
問題の感覚がつかめたところで、勉強方法をまとめましょう。
力の向きと動かした向きを図に描こう
ポイント②で学んだように、仕事の大きさを求めるときには力の向きと物体を動かした向きがとても重要です。
数字だけ見て計算したものの、向きが間違っていた…なんてことにならないよう、2つの向きを図に描き出してから問題に取り組むようにしましょう。
仕事の直前対策法!
それでは具体的に、仕事の直前対策としてどのようなことに取り組めば良いのでしょうか?
他の単元と組み合わせて解けるようにする!
仕事の大きさや仕事率を求める問題のほか、この後の単元で習うエネルギーと組み合わせて出題されることもあります。
そのため、自分に合った問題集などで組み合わされている設問に取り組み、様々なパターンに慣れておきましょう。
単位間違いに注意!
仕事の大きさや仕事率を求めるとき、問題文に示されている距離や時間を使って計算することが多いです。
そのときに気を付けたいのが、単位の換算ミスです。
仕事や仕事率を表す式をおさらいしておきましょう。
![]()

これらの式に出てくる距離の単位は[m]、時間の単位は[s]です。
でも、問題文には距離が[cm]や[km]で書かれていたり、時間の単位が[時間(h)][分]になっていたりすることがあります。
「あとで単位換算しよう」と考えていると、数字を見て安心して単位換算を忘れてしまうこともあり得ます。
計算し始める前に単位をよく見て、必要なら換算することを習慣化しましょう。
まとめ
理科における仕事とはなにか、そして入試ではどのように出題されるのかおわかりいただけたでしょうか?
力の向きと物体を動かす向きをきちんと整理すれば、そう難しいことはありません。
ここで学んだ勉強法を活かして、得点につなげていきましょう!














