理科や小学校の算数で習った「速さ」。
この「速さ」を扱った文章題は、いつの世も多くの中学生を悩ませています。
しかし実はこの「速さ」が中学校の数学の単元やさくいんの中に出てくることはありません。
そのため、教科書だけでは問題演習の機会が少なくなりがちです。
この記事では「速さ」の例題を取り上げながら、考え方やつまずきやすいポイントを徹底解説します!
中学数学における「速さ」とは
速さとは、単位時間あたりの移動距離(道のり)を表す量です。
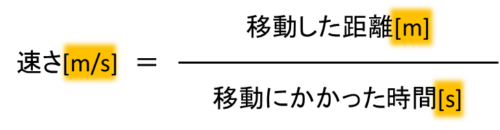
中学数学では、この速さの関係式を使った文章題がよく取り上げられます。
その文章題で必要になる知識は連立方程式(一次)が多いです。
こうした速さを扱った文章題を解くプロセスは、次の2つに大きく分けられます。
- 方程式を作る
- 方程式を解く
このうち、②の方程式を解く部分については連立方程式(一次方程式)の単元でよく練習しておきましょう。
「速さ」を扱った問題でつまずきやすいのは、①の部分です。
なぜなら、①の方程式を作る部分は文章問題などでしか触れることがなく、②に比べて練習量が少なくなりやすいからです。
さらに「速さ」という単元も教科書にはないため、まとめておさらいするのが大変という理由もあります。
そこで、ここでは①の方程式を作る部分について考え方を詳しく解説します。
方程式を作るためのステップ
「速さ」に関する文章題で方程式を作るためには、次のようなステップに分けて考えます。
- 求めるもの、わからないものをx, yとおく
- わかっている情報の単位を揃える
- 線分を描く
- 線分にわかっている情報を書き込む
- 速さの式を使って、わかっているものとわからないものを結び付ける
それでは、各ステップについて例題を交えながら詳しく解説していきます。
自分がどこでつまずいているのか考えながら、よく理解を進めてくださいね。
例題:
テツヤ君の家からのケン君の家の前を通って学校まで1300mある。
テツヤ君が家を出発してからケン君の家までは毎分60mで歩き、
ケン君の家から学校までは毎分40mで歩くと合計で25分かかった。
テツヤ君の家からケン君の家までにかかった時間と、
ケン君の家から学校までにかかった時間をそれぞれ求めよ。
1. 求めるもの、わからないものをx, yとおく
まずは求めたいものをx, yを使って表しましょう。
ここでは、テツヤ君の家からケン君の家までにかかった時間をx、ケン君の家から学校までにかかった時間をyとします。
2. わかっている情報の単位を揃える
この問題でわかっている情報は道のり・時間・速さです。
それぞれ単位は、道のりがm、時間が分、速さがm/分となっています。
そのため、xとyの単位も「分」にそろえましょう。
この段階で、速さに使われている単位は道のりと時間の単位に合わせておきましょう。
3. 線分を描く
「速さ」の出てくる文章題では、線分に情報を書き込むのがポイントです。
線分を中心とした、次のような図を描いてみましょう。
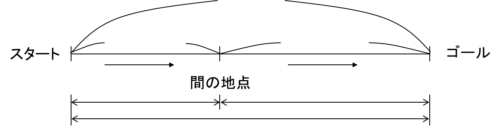
次は、この中にわかっている情報を書き込んでいきます。
コツは「湖の周り」のようにまっすぐではない道や「往復」のルートも線分にすることです!
情報を整理するのが目的なので、道のりがどんな形状であろうとまっすぐ伸ばしてやりましょう。
4. 線分にわかっている情報を書き込む
先ほどの図にわかっている情報を書き込んでいきましょう。
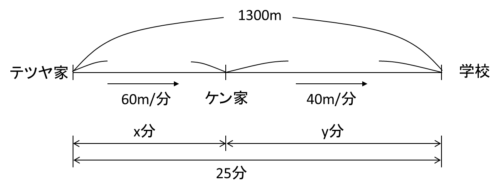
コツは「単位が揃っているかどうか確かめながら書き込むこと」です。
もしこの段階で単位がそろっていなかったら、次のステップに進む前にそろえておきましょう。
5. 速さの式を使って、わかっているものとわからないものを結び付ける
速さの式を使うと、道のり=速さ×時間で表せました。
よって、
テツヤ君の家からケン君の家までの道のり=60x
ケン君の家から学校までの道のり=40y
となります。
これも図に書き込むと、次のようになります。
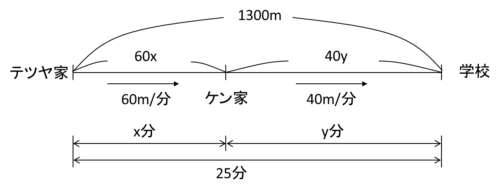
図の空いているところがすべて埋まりましたね。
では、最後に2つの線分から関係式を立ててみましょう。
図から「テツヤ君の家からケン君の家まで+ケン君の家から学校まで=テツヤ君の家から学校まで」であることがわかります。
よって、連立方程式は次のようになります。
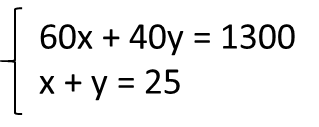
これで①方程式を作るの工程が終わりました。
②方程式を解くはここでは解説を省略しますが、答えは x = 15, y = 10となります。
練習もかねて解いてみてくださいね。
速さの文章題を実際に解いてみよう
それでは、今度は解説なしで実際に問題を解いてみましょう。
“全長50kmのコースを、スタートからA地点までは自転車で進み、A地点から先は自転車を降りて走った。
自転車では時速20km、自転車を降りてからは時速10kmで走って、全体を3時間で完走した。
自転車で進んだ道のりと走った道のりをそれぞれ求めなさい。”
それでは解説です。
ここでも、次のステップに従って解いてみましょう。
- 求めるもの、わからないものをx, yとおく
- わかっている情報の単位を揃える
- 線分を描く
- 線分にわかっている情報を書き込む
- 速さの式を使って、わかっているものとわからないものを結び付ける
今回求めたいものは自転車で進んだ道のりと走った道のりなので、それぞれx, yとおきます。
次に、道のりはkm、時間は「時」で単位がそろっていることを確認します。
続いて線分を書き、そこに情報を書き込みましょう。
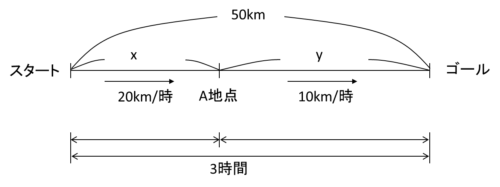
この情報を元に速さの式を使って式を作りましょう。
時間=距離 / 速さで表されるので、図の空いている部分には x / 20, y / 10が入ります。
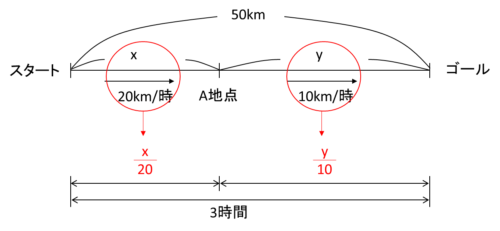
そして、図から連立方程式を立てます。
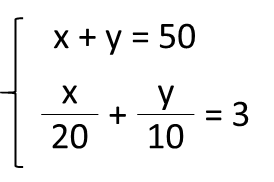
これを解くと( x, y ) = (40, 10)となります。
よって、答えは自転車で進んだ道のりが40km、走った道のりが10kmとなります。
両者の値を足すと確かに全長50kmとなり、問題文に合っていることが確かめられます。
速さの勉強方法
問題の感覚がつかめたところで、勉強方法をまとめましょう。
図に情報を全部書き出そう!
文章問題の難しいところは、たくさんの情報があちこちに散らばって見える点です。
そこで、文章の中に散りばめられている情報は全て図に書き出すようにしてみましょう。
このとき、書き出す段階で単位を統一しておくのがミスを防ぐポイントです。
いろんなパターンの問題に慣れておこう!
「速さ」を扱った問題には、道のり(距離)・速さ・時間という3つの値が出てきます。
これらのうち、どれを求めよと言われても連立方程式が立てられるように、よく練習しておきましょう。
方程式を作るところまで出来れば、あとは方程式を解くだけです。
方程式を解く際にかけ算やわり算を使って係数をそろえるという違いはありますが、そこは計算練習を十分にすれば乗り越えられます。
まずは正しい方程式を作ることを意識して、文章題に取り組みましょう。
速さの直前対策法!
それでは具体的に、速さの直前対策としてどのようなことに取り組めば良いのでしょうか?
直前期に「速さ」の出てくる問題で注意したいのは、単位間違いや計算ミスです。
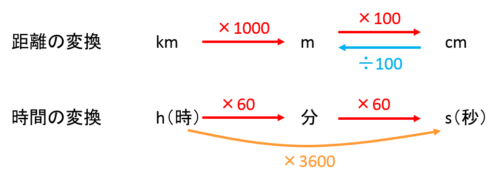
単位換算に慣れておこう!
図に情報を書き出す前に、単位換算することを心がけましょう!
特に、道のりを表すのにkmやmが混在していたり、時間の単位が時・分・秒の複数を使っていたりすることがあります。
こうした場合は、求める値に単位をそろえてから図に記入するようにしましょう。
速さの単位は道のりと時間の単位で表されるので、道のりや時間の単位と合っているかどうかよく確かめることが大切です。
検算するクセをつけよう!
せっかく時間をかけて方程式を作って解いたとしても、計算ミスがあれば得点にはつながりません。
こんなもったいない思いをしないためには「検算」することをおすすめします。
検算と言っても、難しく考える必要はありません。
まずは、一見しておかしい数値がないか確認しましょう。
そして、問題文の中に書かれている内容と答えが合っているか確かめましょう。
こうした確認を習慣化することで、確実にミスは減らせます。
着実に得点につなげ、ライバルに差をつけましょう。
まとめ
中学数学の「速さ」は多くの中学生を苦しめる文章題の代表例です。
考える工程が多いので、どこでつまずいているかわかりにくいのも難しいポイントです。
でも、考え方のステップを一つひとつ丁寧に追っていけば大丈夫。
記事で考え方を確認しながら例題をたくさん解いて、得意分野に変えてくださいね!














