高校受験で必須！数学の証明問題における勉強法について！

都立高校の入試数学に毎年証明の問題が出題されています。

得点差がつきやすく、合否を分ける問題と言うこともできます。

ここでは受験生の保護者の方からの証明問題に対する勉強法を知りたいという要望に応えてみたいと思います。

証明とは

高校入試の問題の一ジャンルとして証明問題があります。

「証明」とは、

「三角形ABPと三角形ACQが相似であることを証明せよ」

のように、問題で指定された事柄が正しいことを条件を挙げて示すことです。

証明を行うための必須条件として、2つの三角形が相似あるいは合同であるための条件を知っていることと、「∠APBと∠AQCが等しい」といった図形のパーツが等しいことを見抜けることが挙げられます。

以下、順を追って、都立高校共通問題における数学の勉強法について解説します。

都立入試における証明の出題傾向

都立入試数学では例年2問程度証明問題が出題されています。

令和2年度（2020年度）では大問2の〔問2〕が数式を用いた証明問題。

大問4の〔問2〕①が三角形の合同を証明する問題でした。

証明は解答が面倒なので差がつきやすい！

2問とも配点は7点で、数学でもっとも配点が大きい問題になっています。

証明問題は、きちんと条件を覚えたうえで、条件が成立する根拠を過不足なく示す必要があります。

正確さが問われ、それを文章で論証しなくてはならず（計算するだけでない）、配点が大きいこととも相まって、得点差がつきやすい問題だといえるでしょう。

証明問題を解く上で覚えておきたいポイント！

図形の証明問題に関して覚えておきたいポイントを説明します。

図形の証明問題は基本的に、三角形の合同条件などの「条件」を「根拠」を挙げて示す、というパターンです。

そのため慣れてしまえばワンパターンであるため得点しやすい問題ともいえます。ポイントを押さえて確実に得点したいところです。

わかったことを図に書き込んでおく！

たいてい、問題には「∠ABPと∠ACQが等しい」といった仮定と、示すべき図が描いてあります。

「角が等しい」「辺の長さが等しい」などわかったことは図に書き込んでいくといいでしょう。

例えば「∠ABP＝∠ACQ」なら下図のように書き込みます。

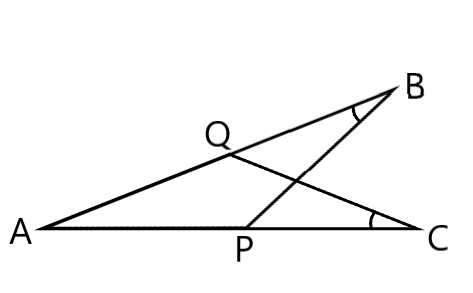
「BP=CP」なら下のように書き込みます。

ある程度証明の流れを暗記する！

図形の証明問題はワンパターンなので、そのパターンを覚えてしまいましょう。

三角形の相似を示すのなら、

「⊿ABPと⊿ACQにおいて
共通だから
∠BAP＝∠CAQ
仮定から
∠APB＝∠AQC
二組の角がそれぞれ等しいので
⊿ABP∽⊿ACQ」

2つの角が等しいことを示して、それが相似の条件だ、と宣言します。

「根拠を示して、条件を言う」

この流れを覚えておくことです。

それから、解答の記入は「∠BAP＝∠CAQ」「∠APB＝∠AQC」の二つの根拠を見抜き、条件が成立することが分かってから始めましょう。

条件が分かる前から記入を始めてしまうと場当たり的な解答になり、途中でやり直して消しゴムで消さなくてはならない、といったこともあり得ます。それを防ぐためにも記入は見抜いてから、です。

採点者が上から順にスムーズに理解できるように書く！

証明問題は答えの値を答えるだけでなく、文章で説明しなくてはいけません。

そのため丁寧な字で書いて、順番に整理して論証の筋道がわかるようにして、採点者にしっかり正しく伝える必要があります。明確な方針を持って解答に臨みましょう。

高校入試で頻出の証明問題は？

都立入試における過去問をあたってみると、図形の証明問題は、三角形の合同を示す問題と三角形の相似を示す問題が頻出です。

過去5年の実績データです。

三角形の合同

2020年度　正方形に関係する三角形の合同
2018年度　円に関係する三角形の合同

三角形の相似

2019年度　平行四辺形に関係する三角形の相似
2017年度　半円と長方形に関係する三角形の相似
2016年度　平行四辺形に関係する三角形の相似

この5年に限ってみれば、図形の証明の問題は、三角形の合同・相似以外出題されていません。

実際にどのような問題が出題されるのか？

2020年度都立高校入試数学の大問４〔問２〕①を解説してみます。

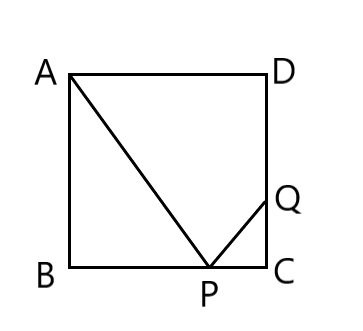
（大問４）右の図1で、四角形ABCDは正方形である。
点Pは辺BC上にある点で、頂点B、頂点Cのいずれにも一致しない。
点Qは辺CD上にある点で、CP=CQである。
頂点Aと点P、点Pと点Qをそれぞれ結ぶ。
次の各問いに答えよ。

図1

〔問1〕割愛
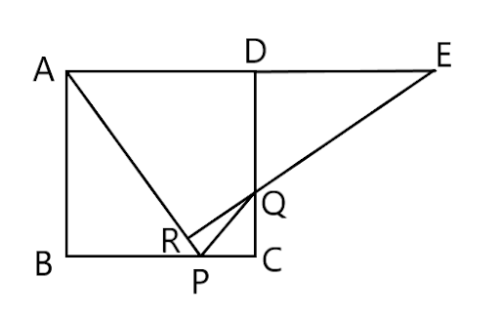
〔問2〕右の図2は、図1において、辺ADをDの方向に延ばした直線上にありAD=DEとなる点をE、点Eと点Qを結んだ線分EQをQの方向に延ばした直線と線分APとの交点をRとした場合を表している。

図2

次の①、②に答えよ。
①△ABP≡△EDQであることを証明せよ。
②割愛

（解説）
仮定よりAD=DE
ABとADは正方形の一辺だから等しい
よってAB=ED

BCとDCは正方形の一辺だから等しい
仮定よりCP=CQ
よってBCーCP＝DCーCQ
∴BP=DQ

また
∠ABP＝∠EDQ（＝90°）

2辺の長さとその間の角が等しいので⊿ABP≡⊿EDQ

根拠「AB=ED」「BP=DQ」「∠ABP＝∠EDQ」を示して、それが
合同条件「2辺の長さとその間の角が等しい」にあてはまることを言う

このように、根拠を挙げて条件を言うということに慣れてしまえば、ワンパターンで単純です。

なお、都の発表によるとこの問題の正答率は65.7％でした。

また、証明問題は部分点がもらえるので、全部は解けない場合でも根拠の一部を示して得点を狙いましょう。

証明問題の勉強方法について

証明問題の勉強において大切なのは以下の4点です。

• 合同条件と相似条件を覚える
• 問題文や図を見て等しい箇所を見抜く
• 様々な問題を解きパターンを覚える
• 教科書や参考書の解説を丁寧に読み込む

合同条件と相似条件を覚える

まず、合同条件、相似条件、これは正確に覚えておかなくてはいけません。

三角形の合同条件

1. 3組の辺の長さがそれぞれ等しい
2. 2組の辺の長さとその間の角がそれぞれ等しい
3. 1組の辺の長さとその両端の角がそれぞれ等しい

三角形の相似条件

1. 2組の角がそれぞれ等しい
2. 3組の辺の長さの比がそれぞれ等しい
3. 2組の辺の長さの比とその間の角がそれぞれ等しい

覚え方のコツですが、条件のひとつは3辺の関係（合同の①、相似の②）で、残りのふたつはサンドイッチ（2辺の間、2角の間）のイメージです。

なお、出題される相似の問題で用いる条件にかたよりがあって、①の2組の角が等しいを用いるパターンがほとんどです（おそらく比を設定するのが難しいためか）。2016、2017、2019いずれもそうでした。

問題文や図を見て等しい箇所を見抜く

それから、問題文・図を見て、「辺の長さが等しい」「角が等しい」といったことを見抜けなければいけません。

それらには

1. 角、辺を共有している
2. 問題文に仮定してある
3. 図形の基本的な性質

があります。

①②は見れば分かるとして、③が大切です。

中学数学で出てくる基本的な図形の性質を挙げてみると

• 対頂角
• 平行線の同位角、錯角
• 二等辺三角形、正三角形の性質
• 平行四辺形の性質
• 円の性質

これらのものがあります。

図形のパーツが等しいことを見抜いたうえで、それを合同条件、相似条件にあてはめることが求められます。

そういうことを頭におきながら、学習してください。

様々な問題を解きパターンを覚える

合同条件、相似条件、図形上で等しいパーツ、を覚えて使えなければいけません。

そのために条件の文章を読んでただ暗記するというよりは、実際に様々な問題を解いてみてこういうふうに使うのか、と体感することが大切です。

多くの練習問題をやればパターンだけでなくなにが大切なのかが見えてきます。

教科書や参考書の解説を丁寧に読み込む

練習問題を解いたら、模範解答を見て次のことを確認します。

• 合同条件・相似条件を正しく扱えているか
• 根拠を漏れなく挙げられているか

教科書、参考書・問題集の解説を丁寧に読み込みましょう。

証明の直前対策法！

試験直前には、合同条件①～③と相似条件①～③、対頂角、同位角、錯角、二等辺三角形の性質、平行四辺形の性質、円の性質を確認しましょう。

そして、図形の証明のパターンを思い出しましょう。

まとめ

• 都立高校の入試数学には毎年証明問題が出題される。また、その配点が大きい
• 証明問題は差がつきやすい問題である
• 証明問題はワンパターンなので、そのパターンを覚えてしまえば得点できる
• パターンは「根拠を示して、条件にあてはめる」
• 合同条件、相似条件、対頂角、同位角、錯角、二等辺三角形の性質、平行四辺形の性質、円の性質などを正確に覚える必要がある
• 多くの練習問題にあたってパターンを習得する