二次関数の一種、関数 $y = ax^2$ は都立高校入試でも頻出の単元です。
2年に1回程度の割合で大問が出題されているので、苦手意識は早めになくしておきましょう!
二次関数とは
今回の記事では、二次関数の一種である関数 $y = ax^2$ について解説します。
二次関数とは、 $y = ax^2 + bx + c$ のような2次式で表される関数のことです。
より数学的に表現すると「 $y$ が $x$ の関数で、2次式 $y = ax^2 + bx + c$ で表されるとき、 $y$ は $x$ の2次関数である」となります。
このような二次関数のうち、中学数学では、 $y = ax^2$ という $b$ と $c$ が0である特別な場合について学びます。
以下、この記事では「二次関数は関数 $y = ax^2$ を指す」ものとします。
二次関数と比例・反比例・一次関数の違い
二次関数は、比例・反比例・一次関数といったそれまでに習った関数ではとらえられない関数です。
二次関数で表されるものには、次のような例があります。
- ジェットコースターの進む距離 $y$ と時間 $x$ の関係
- 斜面で球を転がしたときの距離 $y$ と時間 $x$ の関係
- 物体が落下するときの距離 $y$ と時間 $x$ の関係
こういった場合の $x$ と $y$ の値を調べて表にすると、 $y$ は $x$ の値に連動して決まることがわかります。
しかし、 $x$ と $y$ の関係が比例・反比例・一次関数のどれにもあてはまらないため、こうした例を表すには他の関数が必要なのです。
そこで $x$ の2乗( $x^2$ )と $y$ の関係性を見てみると、 $y$ が $x^2$ に比例していることがわかります。
$y$ が $x$ の関数で $y = ax^2$ という式で表されるとき、文字 $a$ を「比例定数」といいます。
二次関数の問題では、$x \neq 0$ のとき、比例定数 $a$ は $a = \frac{y}{x^2}$ で求められます。
二次関数のグラフ
二次関数のグラフは「放物線(ほうぶつせん)」と呼ばれます。
これは、物体を放り投げたときに描く軌跡が二次関数のグラフの形になるためです。
ここで先ほど挙げた例を見てみると、物体の運動を表すときに二次関数が必要なことがよくわかるのではないでしょうか。
「二次関数」という言葉にとっつきにくい印象を持っている方は、実は身近な関数なんだととらえて気楽に勉強を進めてくださいね。
二次関数のグラフの特徴
さて、そんな二次関数のグラフには次のような特徴があります。
- 原点を通る( $x = 0$ のとき $y = 0$ )
- $y$ 軸について対称である( $y$ 軸で折り返すと重なる)
- $a \gt 0$ のときは上に開いた形、 $a \lt 0$ のときは下に開いた形になる
- $a$ の値の絶対値が大きいほど、グラフの開き方は小さい
この特徴は、 $y$ と $x$ の関係が二次関数であるかどうかを見極める大切なポイントなので、確実に覚えておきましょう。
もしわからなくなったら、実際におおまかなグラフを描いてみましょう。 グラフを描くことに慣れてくれば、自然と特徴が頭に入ってくるようになりますよ。
二次関数でよく出される問題
では、二次関数についてどんな問題がよく出されるのか見ていきましょう。
変化の割合を求める問題
二次関数と一次関数の大きな違いは、変化の割合が一定ではないということです。
そのため、二次関数の変化の割合を求める問題がよく出題されます。
この変化の割合は、 $y$ の変化量を $x$ の変化量で割ることで求められます。
例えば、 $y = 2 x ^ 2$ という関数で $x$ が1から3へと増加するときの変化の割合を考えてみましょう。
$x$ は1から3へと変化するので、 $x$ の変化量は $3 – 1 = 2$ です。
$x = 1$ のとき、 $y = 2 \times ( 1 ^ 2 ) = 2$
$x = 3$ のとき、 $y = 2 \times ( 3 ^ 2 ) = 18$
なので、 $y$ の変化量は $18 – 2 = 16$ です。
よって、この場合、変化の割合は $16 \div 2 = 8$ となります。
この値は「変化前の座標 $( 1, 2 )$ と変化後の座標 $( 3, 18 )$ の2点を通る直線の傾きと一致する」ということを押さえておきましょう。
変域を求める問題
こちらは、 $x$ をある範囲で動かしたとき、 $y$ がとりうる値の範囲を求める問題です。
変化の割合を求める問題と似ていますが、変域を求める問題では注意したいことが1つあります。
それは「原点を含む場合」です。
$y = 3 x ^ 2$ という関数を考えてみましょう。
$x$ の変域が $-1 \leqq x \leqq 2$ のように $x = 0$ を含んでいる場合、 $y$ の変域はどうなるでしょうか?
まず、変域の両端における $y$ の値を求めてみましょう。
$x = -1$ のとき、 $y = 3 \times ( -1 ) ^ 2 = 3$
$x = 2$ のとき、 $y = 3 \times 2 ^ 2 = 12$
そのため「 $y$ の変域は $3 \leqq y \leqq 12$ だ」と考えてしまいがちですが、関数 $y = 3x^2$ は「必ず原点を通る」ので、 $y$ は $x = 0$ のときに0となります。
よって、正解は $0 \leqq y \leqq 12$ です。
このミスを防ぐには、
- $x$ の変域が原点を含んでいるかどうか考える
- おおまかでいいのでグラフを描いてみる
というのが大切なポイントです。
文章題
二次関数で表される代表例として物体の運動を挙げましたが、こうした運動を例にとった文章題もよく問われます。
物体の落下や振り子の運動に関する文章題を見かけたら、二次関数の問題かもしれないと意識するようにしましょう。
他の単元との組合せ問題
二次関数は、一次関数など他の単元と組み合わせて出題されることもよくあります。
さらに、二次関数と一次関数の交点で作られた三角形の面積を求めるなど、図形問題と組み合わされる問題も出ています。
過去問などで複合的な問題に触れておくようにしましょう。
二次関数の入試問題を解いてみよう
それでは、実際の入試問題を解いてみましょう。
次の問題は、令和2年度都立高校入試大問3から抜粋したものです。
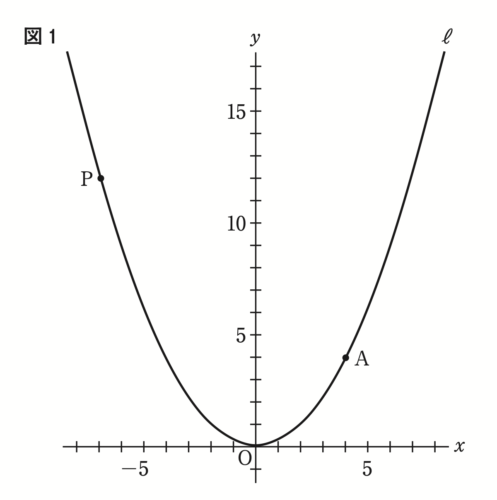
下の図1で、点 $O$ は原点、曲線 $l$ は関数 $y = \frac{1}{4} x ^ 2$ のグラフを表している。
点 $A$ は曲線 $l$ 上にあり、 $x$ 座標は4である。
曲線 $l$ 上にある点を $P$ とする。
次の問に答えよ。[問]次の①と②に当てはまる数を、下のア~クのうちからそれぞれ選び、記号で答えよ。
点Pの $x$ 座標を $a$ 、 $y$ 座標を $b$ とする。
$a$ のとる値の範囲が $-8 \leqq a \leqq 2$ のとき、 $b$ のとる値の範囲は、① $\leqq b \leqq$ ②である。ア -64 イ -2
ウ 0 エ 1/2
オ 1 カ 4
キ 16 ク 64
では、さっそく解いていきましょう。
点Pの $x$ 座標が $a$ 、 $y$ 座標が $b$ ということなので、 $a$ の範囲が $-8 \leqq a \leqq 2$ であるということは、点 $P$ の $x$ 座標の変域が $-8 \leqq a \leqq 2$ という意味です。
つまり、これは点 $P$ の $y$ 座標の変域を求める問題です。
変域の問題では、 $x$ のとりうる値が0を含むかどうかに注意しましょう。
グラフの該当部分を太く塗るなどして、可視化(見える化)するとわかりやすくなります。
今回は上に開いた放物線で、 $x$ の変域が0を含むため、 $y$ の変域の最小値は0です。
よって、①はウだとわかります。
つぎに、 $y$ がとりうる値の最大値を考えましょう。
$x$ の変域の最大値と最小値のうち、絶対値が大きいのは $x = -8$ のほうですね。
このとき、$y = \frac{1}{4} \times ( -8 ) ^ 2 = 16$ となるので、②に当てはまるのはキです。
最後にグラフでおおまかな値を読み取って、答えがあっていそうか確かめるとミスが少なくなりますよ。
二次関数の勉強方法
問題の感覚がつかめたところで、勉強方法をまとめましょう。
グラフを描いてみよう!
二次関数の理解やケアレスミス対策には、グラフを描くことが大切です。
おおまかな形でもいいので、グラフを描いて考えることに慣れておきましょう。
二次関数の直前対策法!
それでは具体的に、二次関数の直前対策としてどのようなことに取り組めば良いのでしょうか?
いろんなパターンの問題に慣れておこう!
この記事で解説しただけでも、大きく分けて4種類の出題パターンがありましたね。
過去問や問題集でいろんなパターンの問題に取り組んで、いざというときに戸惑わないよう練習を重ねておきましょう。
まとめ
いかがでしたでしょうか?
苦手な部分を早めになくして、二次関数を得点源にしていきましょう!