今回の記事では「エネルギー保存の法則」について解説していきます。
「エネルギー保存の法則って?力学的エネルギー保存の法則とかいうのも聞いたことがあるけどそれのこと?」
そんなふうに思っている方こそ、この記事を読んで曖昧な部分をしっかり整理しましょう!
エネルギー保存の法則とは
エネルギー保存の法則には、実は2種類あります。
力学的エネルギー保存の法則
1つめは「力学的エネルギー保存の法則」です。
これは「外部から力を受けない限り力学的エネルギーは一定に保たれる」という法則で、次のように表されます。
力学的エネルギー=位置エネルギー+運動エネルギー=一定
エネルギー保存の法則
2つめは「エネルギー保存の法則」です。
こちらには「力学的」という言葉がないことに注目しましょう。
これは、「エネルギーの種類が移り変わってもエネルギーの総和は変わらない」という法則です。
これら2つの法則がどう違うのか、それぞれの意味を詳しく見ていきましょう。
エネルギー保存の法則を理解する上で覚えておきたいポイント!
ここからはエネルギー保存の法則を理解するために押さえておきたいポイントをご紹介します。
- ポイント①エネルギーとはなにか押さえよう
- ポイント②力学的エネルギーは「位置エネルギー」+「運動エネルギー」
- ポイント③力学的エネルギー保存の法則を理解しよう!
- ポイント④「力学的」のつかないエネルギー保存の法則を理解しよう!
では、順番に見ていきましょう。
ポイント①エネルギーとはなにか押さえよう
そもそも「エネルギー」とは?
理科では「ある物体がほかの物体に対して仕事をする能力」のことをいいます。
つまり、物体が仕事のできる状態にあるとき「その物体はエネルギーをもっている」といいます。
少し抽象的で難しいですね。
具体的に「ある物体がほかの物体に対して仕事をする」というのは、例えば
- ほかの物体を移動させる
- ほかの物体を変形させる
- ほかの物体を壊す
ということです。
理科でいう仕事では、物体が力の向きに動きましたね。
ぶつかった相手が木片だったら動きますが、壁だったら動かせないので、へこんだり壊れたりしてしまいます。
このように、ほかの物体に影響を与える能力のことを「エネルギー」といいます。
エネルギーの単位も仕事と同じ[J](ジュール)です。
仕事をすると、その分だけ物体のもつエネルギーは減って小さくなります。
物体がした仕事の大きさを求めることで、その物体がもっていたエネルギーの大きさがわかります。
ポイント②力学的エネルギーは「位置エネルギー+運動エネルギー」
では、力学的エネルギーとはどんなエネルギーなのでしょうか?
- 位置エネルギー:高いところにある物体がもつエネルギー
- 運動エネルギー:運動している物体がもつエネルギー
これらを合わせて「力学的エネルギー」といいます。
それぞれについて詳しく見ていきましょう。
位置エネルギー
位置エネルギーは次のように表されます。

この公式を使って、図のような場合の位置エネルギーを考えてみましょう。
ここで100gの物体の重さが1Nであることに注意しましょう。
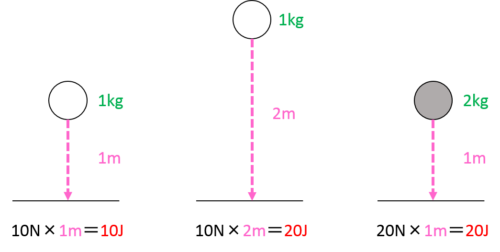
この公式から、位置エネルギーの大きさは質量と高さに比例することがわかります。

「あれ?重さじゃなくて質量?」と思った方はいい着眼点を持っています。
位置エネルギーは物体の重さに比例しますが、物体の重さは質量に比例するので、位置エネルギーは質量にも比例するのです。
重さは[N]、質量は[kg]や[g]と単位が異なるので、計算の際は注意しましょう。
位置エネルギーの例には、高いところからおもりを落とす場合や水力発電などがあります。
運動エネルギー
運動エネルギーは運動している物体のもつエネルギーで、質量に比例し、速度の2乗に比例します。
運動エネルギーにも公式がありますが、少し発展的な内容なので、中学理科では力学的エネルギーと位置エネルギーから求められれば十分です。
速度に比例するのではなく、速度の2乗に比例するという点だけ注意しておきましょう。
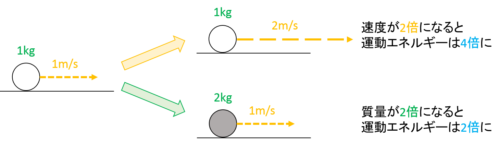

運動エネルギーの例には、斜面を滑り下りる台車の運動やジェットコースターなどがあります。
ポイント③力学的エネルギー保存の法則を理解しよう!
さて、力学的エネルギーの正体がわかったところで「力学的エネルギー保存の法則」について整理しましょう。
これは「外部から力を受けない限り力学的エネルギーは運動している間も常に一定である」という法則です。
力学的エネルギー保存の法則は次のように表されます。
![]()
例えば、坂道の一番上から自転車で坂道をくだる場面を考えてみましょう。
坂道の上にいるとき、坂道の高さ分だけ位置エネルギーをもっています。
この状態で坂道をおり始めると、自転車をこがなくても走りだしますよね。
このとき位置エネルギーが運動エネルギーに変化していますが、坂道をくだっている間ずっと位置エネルギーと運動エネルギーの和は変わりません。
これが力学的エネルギー保存の法則です。
ここで、よく出題される運動を2つ解説します。
斜面を下る運動
台車が斜面を下る運動をしているとき、位置エネルギーと運動エネルギーの変化は次の図のようになっています。

運動の途中で位置エネルギーが運動エネルギーに変化しても、力学的エネルギーは常に一定に保たれています。
振り子の運動
振り子の運動では、位置エネルギーと運動エネルギーの変化は次の図のようになっています。
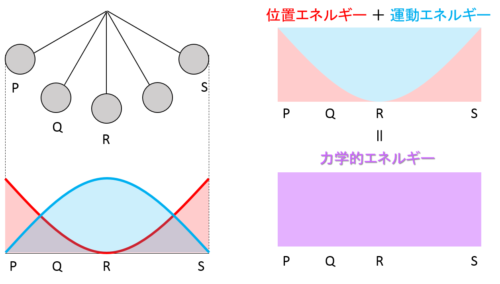
この場合も、斜面の運動とグラフの形は変わりますが、力学的エネルギーが常に一定であることは変わりません。
このように運動の様子を示した図に合わせて点線を引いて、エネルギーの変化を示したグラフを描くとわかりやすくなります。
ポイント④「力学的」のつかないエネルギー保存の法則を理解しよう!
ここで注意したいことがひとつあります。
それは、力学的エネルギー保存の法則には「外部から力を受けない限り」という条件がついていることです。
振り子がそのうち止まるように、摩擦力や空気抵抗があると力学的エネルギーは保存しません。
坂道を自転車でくだる例でも、実際には摩擦力や空気抵抗を受けてだんだんスピードが落ち、やがては止まってしまいますよね。
こうした運動に影響を与える力がはたらいている場合、エネルギーはどうなるのでしょうか?
実は、「力学的」のつかない「エネルギー保存の法則」があるのです。
これまでに習った電気エネルギーのように、力学的エネルギー以外にもいろんな種類のエネルギーがあります。
- 弾性エネルギー
- 電気エネルギー
- 熱エネルギー
- 光エネルギー
- 化学エネルギー
- 音エネルギー
- 核エネルギー
こういったエネルギーの種類は、いろんな装置を使って変換することができます。
しかし、エネルギーの種類が移り変わってもエネルギーの総和は変わりません。
これを「エネルギー保存の法則」といいます。
例えば、照明器具は電気エネルギーを光エネルギーに変換しています。
しかし、電気エネルギーが100%光エネルギーになっているわけではなく、一部は熱エネルギーになって逃げてしまいます。
電球を触ると温かいのはそのためです。
でも、変換された光エネルギーや熱エネルギーの総和は、変換前の電気エネルギーの総和と変わらない。
これが「力学的」と付かないほうの「エネルギー保存の法則」です。
実際にどのような問題が出題されるのか?
それでは実際の入試問題を解いてみましょう。
以下の問題は、平27年度都立高校入試の大問6から抜粋したものです。
“(1)質量1kgの力学台車と、質量500gのおもり、滑車、糸を用意した。実験に使用する滑車と糸の質量や摩擦は考えないものとする。
(2)図のように、一端をスタンドに結び付けた糸を、動滑車と2個の定滑車に通し、他端を水平な床の上に置いた力学台車に結び付けた。
(3)動滑車におもりを付けた。
(4)糸を張った状態で、図の矢印の向きに力を加えて力学台車を動かし、おもりが床から30cmの高さになったところで、静止させた。
(5)手を離したところ、おもりと力学台車は同時に動き出した。
おもりを30cm持ち上げるために必要な仕事の大きさと、おもりが落下し始めてから床に達するまでの間、おもりと力学台車がもつエネルギーの移り変わりの様子を組み合わせたものとして適切なのは、次の表のア~エのうちではどれか。”
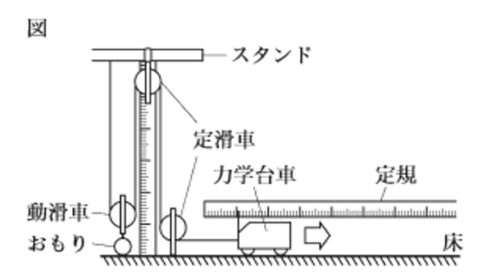

では、早速解いていきましょう。
「おもりを30cm持ち上げるために必要な仕事の大きさ=おもりを30cm持ち上げたときのおもりの位置エネルギー」なので、位置エネルギーの計算式を使いましょう。
おもりの質量は500gなので、おもりの重さは5N、30cm=0.3mです。
よって、おもりの位置エネルギー[J]=5[N]×0.3[m]=1.5[J]となり、選択肢はアかイに絞られます。
このようにおもりが落下し始めたときおもりは位置エネルギーをもっていますが、力学台車はずっと床にある=床からの高さが0なので位置エネルギーをもっていません。
つまり、おもりと力学台車の運動エネルギーはおもりの位置エネルギーから変化したものであるといえます。
よって、正解の選択肢はイです。
エネルギー保存の法則の勉強方法について
問題の感覚がつかめたところで、勉強方法をまとめましょう。
エネルギーの変化を図に描こう!
運動の様子を示した図に合わせてエネルギーの変化を示したグラフを描くと、変化が目に見えてわかりやすくなります。
縦と横の目盛りをきちんと描かなくても、だいたいのエネルギーの増減を描いてイメージできればOKです。
エネルギー保存の法則の直前対策法!
それでは具体的に、エネルギー保存の法則の直前対策としてどのようなことに取り組めば良いのでしょうか?
位置エネルギーの計算方法を覚える!

この公式はエネルギーの大きさを求めるのに必須なので、しっかり覚えておきましょう。
運動エネルギーの求め方を覚える!
運動エネルギーを表す式は少し発展的な内容になるので、ここではその式は使わず「力学的エネルギー保存の法則」を用いた求め方を覚えておきましょう。
力学的エネルギー保存の法則を変形すると、運動エネルギーは次の式で求められます。
![]()
位置エネルギーを使って算出する方法をしっかり覚えておきましょう。
よく出るパターンに慣れておく!
ポイント③でまとめた「斜面を下る運動」と「振り子の運動」はよく出題されるので、過去問や問題集などで慣れておきましょう。
まとめ
エネルギー保存の法則は、物体の運動の分野でよく出題されるテーマのひとつです。
「力学的」が付くかどうかで意味合いが異なることを整理しておきましょう。
そんなに難しい計算問題ではないので、位置エネルギーと運動エネルギーの算出方法をしっかり覚えて得点につなげましょう!














