空間図形は難しくない！平面との関係性を考え、効果的に勉強しよう！

図形問題の集大成とも言える空間図形。

「紙の上で見ているだけじゃイメージしにくい」と、苦手意識を持つ方も多いです。

でも身の周りを見てみれば、たくさんの空間図形があります。

いま勉強に使っている机、椅子、パソコン、教科書だって、厚みを持つ立体です。

数学において空間図形を理解することは、受験勉強だけでなく実生活においても役立ちます。

ここで空間図形の苦手意識をなくして、得意分野に変えていきましょう！

空間図形とは

空間図形とは、その名の通り空間における図形すべてのことを指します。

そのため厚みのある立体だけでなく、直線や平面も空間図形に含まれます。

そこに「厚みが加わっても、空間図形は平面、線、点で作られている！」ということを押さえておきましょう。

構成要素に分けてしまうのが、空間図形を理解するコツです。

空間図形を解く上で覚えておきたいポイント！

ここで、空間図形を構成している平面、線、点の関係を整理しましょう。

ポイント①平面と点の関係を押さえる

いきなり立体的に考えるのではなく、まずは平面からゆっくり理解しましょう。

そもそも平面とは、どうやって決まるものなのでしょうか？

平面図形で学んだように、直線は異なる2点によって決められます。

そして空間における平面を決めるには、もう1つ点が必要です。

これを図で見てみましょう。

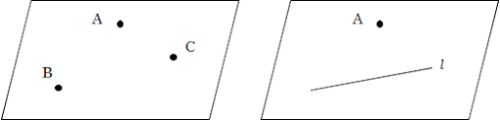
上図のように「1直線上にない3点」によって、平面は決まります。

前述のとおり、異なる2点によって直線が決まるので、右図のように「1直線とその上にない1点」も1つの平面を決定します。

言い換えれば、「1直線上にない3点」を通る平面も、「1直線とその上にない1点」を通る平面も1つであるということです。

ポイント②平面と平面の関係を押さえる

次に、空間におけるその平面同士の関係を見ていきます。

空間における異なる2平面P, Qの位置関係は、「交わる」か「平行である」のどちらかです。

左図が「交わる」場合。平面Pと平面Qが共有する部分は直線で、それを平面Pと平面Qの交線といいます。

右図のように平面Pと平面Qが交線をもたない場合、平面Pと平面Qは「平行である」といいます。

ポイント③直線と直線の関係（ねじれの位置）を押さえる

では、続いて空間における直線と直線の位置関係を考えてみましょう。

空間における異なる2直線l, mの位置関係は3種類に分けられます。それぞれ

• 交わる
• 平行である
• ねじれの位置にある

と言います。

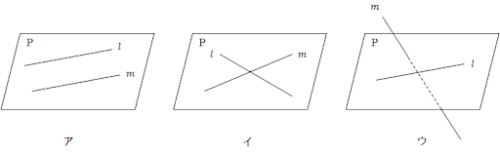
上の図のうち、

• アが空間においても「平行である」状態
• イが空間においても「交わる」状態
• ウが「ねじれの位置にある」状態

を示しています。

このうち、アとイのように2直線が「交わる」か「平行である」場合、2直線は同一平面上にあります。

つまり「平行な2直線」と「交わる2直線」でも、1つの平面を決定することができます。

アとウで示した「平行である」場合と「ねじれの位置にある」場合は、直線同士が共有点を持たないことも覚えておきましょう。

ポイント④平面と直線の関係を押さえる

平面同士、直線同士の位置関係がわかったら、もうひとふんばりです。

最後に、平面と直線の位置関係を考えていきましょう。

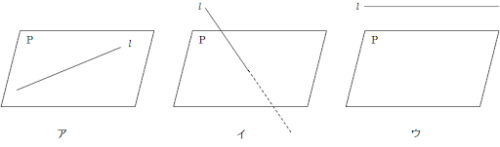
下の図では、

• アは直線が平面上にある（平面に含まれる）場合
• イは直線と平面が1点だけ共有点（これを交点といいます）をもつ場合
• ウは直線と平面の交点がなく、平行である場合

を示しています。

ウのように平行である場合、平面と直線をどこまで伸ばしても交わらないとイメージしてください。

ここまでで平面と直線、点の位置関係を見てきました。お疲れさまでした！

あとは実際に空間図形の問題を解きながら、どことどこが平行か、または交わっているのか判断したり、平面はどこにあるか見つけたりする練習を重ねましょう。

立体図から平面が見つけられるようになれば、もう空間図形は解けたも同然です。

実際にどのような問題が出題されるのか？

さて、それでは実際の入試問題を解いてみましょう。

都立高校入試ではここ数年、大問5に空間図形が出題されています。

以下の問題は、平成30年度都立高校入試の大問5から抜粋したものです。

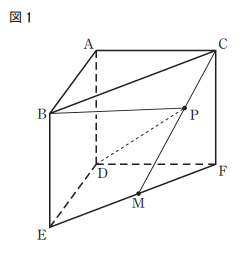
上の図に示した立体ABC-DEFは、
AB=AC=AD=9 cm,
∠BAC=∠BAD=∠CAD=90°の三角柱
である。
辺EFの中点をMとする。
頂点Cと点Mを結び、線分CM上にある点をPとする。
頂点Bと点P、頂点Dと点Pをそれぞれ結ぶ。
図において、点Pが頂点Cに一致するとき、∠BPDの大きさは、〇度である。
〇に当てはまる数字を答えよ。

では、早速解いていきましょう。

図1において、点Pが頂点Cに一致するとき、つまり点P＝点Cのとき、求める∠BPD＝∠BCDです。

「立体の中の角度なんてイメージできない」と思われるかもしれませんが、点B, C, Dに注目すると、この3点で三角形BCDが作られていることがわかります。

このように空間図形の問題が、ただの三角形の内角を求める問題になりました。

抜き出した三角形BCDについて考えてみましょう。この三角形を構成する辺のうち、BCは直角二等辺三角形ABCの斜辺で、この二等辺の長さは共に9 cmです。

CDは一辺9 cmの正方形ACFDの対角線、DBは一辺9 cmの正方形ABEDの対角線です。

つまり、BC, CD, DBはいずれも一辺9 cmの正方形の対角線なので、BC=CD=DBが成り立ちます。

三角形BCDは正三角形なので、答えは∠BPD=60°だとわかります。

いかがでしょうか？

空間図形の問題も、平面を抜き出せば平面図形の問題です。

そこに気付けば、空間図形はもう怖くありません。

空間図形の勉強方法について

出題傾向がつかめたところで、効果的な勉強方法を学びましょう。

図形の断面図でイメトレ！

先ほどの過去問で活用したテクニックは、”平面を抜き出して考える”というものです。

空間図形を空間図形として、つまり立体的なものとしてイメージするのは難しくても、問題を解く際に使うのは一部の平面の組み合わせです。

そのため立体から平面を見つけ出すイメトレが、空間図形に効果的な勉強法なのです。

この際に、イメージするだけでなく「問題を解くときは断面図を書き出す」練習もしておきましょう！

下図のように、立体を正面から見た図を立面図、真上から見た図を平面図といい、それらを組み合わせたものを投影図といいます。

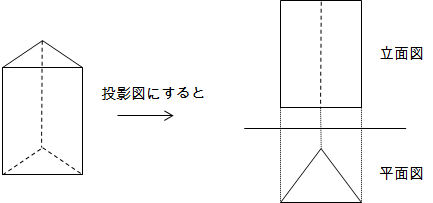
お菓子の箱やサンドイッチなど、立体は身近にたくさんあります。

そうした立体をいろんな角度から眺めたり、断面図や平面図を切り出して、あるいはさらにその一部を抜き出して図に描いてみたり、いろいろイメトレしてみましょう。

空間図形の直前対策法！

場数を踏むことで、空間図形から平面を抜き出すことも、抜き出して出てくるのはどんな図形が多いかも傾向がつかめてきます。

過去問をいくつか解いてある程度のパターンを頭に入れておくと、本番でどんな空間図形が出ても焦らずに済みます。

まとめ

空間図形は中1の範囲なので、早い段階で苦手意識を持つとつらいです。

しかし空間図形も、分解していけば平面と直線と点だということをもう知っていますよね。

平面と直線と点の位置関係を理解できれば、空間図形は難しくありません。

今のうちにきちんと理解して、自信を持って空間図形に挑みましょう！